If you have a question about the Mathematics standards, please try to ask it by creating a new topic in the forum (also accessible from the link in the black navigation bar above). You can search the forum using the Search Forum box on the right.
298 thoughts on “General questions about the Mathematics standards”
Comments are closed.
In my office we have relied a lot on the Progressions Documents to help clarify some confusion with the CCSS. However, many of them are still in draft form, and some are still yet to be released in draft form. When can we expect the Progressions for Geometry, the other part of Measurement and Data, and other Progressions to be released and/or finalized?
Geometry K-6 and the Measurement part of MD should be out by the end of this month, along with high school Statistics and Probability. All of the progressions will be out in draft form by the end of the Summer.
I am glad to hear that but a question I have relates to 6.G.2 which refers to the volume of a right rectangular prism. It states “Find the volume of a right rectangular prism with fractional edge lengths by packing it with unit cubes of the appropriate unit fraction edge lengths, and show that the volume is the same as would be found by multiplying the edge lengths of the prism. Apply the formulas v=lwh and V=Bh to find the volume of right rectangular prisms with fractional edge lengths in the context of real-world problems”.
Since it says apply the formulas does that mean that a student might be given the volume and two sides and be asked to find the other side? Also if it is a cube would they then be expected to find the cube root to determine the side given the volume? I would appreeciate hearing your thoughts on this matter as it has been brought to my attention by a sixth grade teacher. The Model Content Frameworks and the Illustrative Mathematics websites do help but we need more examples to clarify the depth of knowledge needed at each level.
Hi. Any chance the end of the month is here yet? 🙂 Or is there any chance I could steal a glance at the k-2 portion? I am ready to begin writing a unit of study for 1st grade geometry and would love to read and study this before I begin. 🙂
Can you explain the difference between “mentally add and subtract” and “fluently add and subtract”?
Fluent means “fast and accurate” and mental means “in your head”. A fluent calculation is not necessarily mental; a student could be fluent with a paper and pencil algorithm, for example. And a mental calculation is not necessarily fluent, although I think in all of the instances where this phrase is used in the standards fluency is expected as well. But it might be a valuable exercise for a student to mentally add 2 two-digit numbers, even if the calculus is not very fast.
What is the scope of teaching money in grades 2 and 4 when the standards occur before decimals are introduced?
2.MD.8. Solve word problems involving dollar bills, quarters, dimes, nickels, and pennies, using $ and ¢ symbols appropriately. Example: If you have 2 dimes and 3 pennies, how many cents do you have?
4.MD.2. Use the four operations to solve word problems involving distances, intervals of time, liquid volumes, masses of objects, and money, including problems involving simple fractions or decimals, and problems that require expressing measurements given in a larger unit in terms of a smaller unit. Represent measurement quantities using diagrams such as number line diagrams that feature a measurement scale.
I don’t know if this is right or not, but I’ve been encouraging teachers in 2nd grade to work with just cents or just dollars as an application of whole number addition and subtraction. This could also be a good opportunity to apply the properties of operations and counting on strategies.
In 4th grade I see the connection to decimal fractions in NF.5-7. Would you present these measurement problems using the decimal fractions rather than the algorithms for decimal operations? Would the operations performed on these decimal fractions be limited to what the standards have addressed up to this point (addition and subtraction with like denominators and multiplication of a whole number and a fraction)?
Erin basically has it right. In Grade 2 students are dealing with whole number quantities, so word problems for 2.MD.8 would either deal with whole number amounts of dollars or whole number amounts of cents. This doesn’t exclude problems where students have to convert collections of coins and dollars into whole numbers of cents. Indeed, this provides valuable preparation for 4.MD.2.
2.NBT.7 After reading chapter 1 of Liping Ma’s book Knowing and Teaching Elementary Mathematics, I think I see a bit better where this standard is going, but I’m not sure if I clearly understand it yet. According to the progressions document on NBT, the standard algorithm is not required in 2nd grade. Mastery of the algorithm in 4th grade grows out the repeated reasoning drawn from the work the students do in K-3.
The inclusion of language such as “composing and decomposing a ten” (hundred, etc.) and the exclusion of language such as “carry a 1” and “borrow” is intentional? Are the standards intending for teachers to avoid explanations that involve the terms carry and borrow? I see how composing and decomposing are more conceptually-sound terms; I just want to make sure I’m interpreting the intention of the standards correctly
Erin, yes, you have the right interpretation. The standard algorithm builds on a solid understanding of composing and decomposing a ten. Although it is not required in Grade 2, it is not forbidden either. Basically, anything that can get students to a solid understanding of the base ten system in general is worthwhile. For example, carrying and borrowing are words we normally use to describe what elementary school teachers might do with their students. But I think it’s fine for teachers to abandon these words in the presence of true conceptual understanding. [Corrected 4/5/2012.]
Thanks, Bill, for your response. Also in standard 2.NBT.7, I was wondering what was expected by the statement, “relate the strategy to a written method.” What types of written methods does this standard refer to? I was thinking that the students should have a way to capture their mathematical thinking in writing and the problem it represents (knowing how to show a sketch of the base 10 materials and connect it to the written problem 125 +241 = 366), but I wasn’t sure. Thanks for your help.
I am looking for some guidance regarding what the expectation is for N-RN.3. It says to “explain why the sum or product of … is rational; …..that the sum of a rational number and an irrational number is irrational; …” How much is expected at this level? If a student is given an item for this standard will the student response include much more than the definition as a way of explaining?
Here is my interpretation of what this standard requires students to understand and be able to do:
N-RN.3. Explain why the sum or product of two rational numbers is rational; that the sum of a rational number and an irrational number is irrational; and that the product of a nonzero rational number and an irrational number is irrational.
First, review of definition: a real number x is rational if and only if bx=a for some integer a and some non-zero integer b; in other words, it means x is the ratio a/b of two integers, the denominator being non-zero.
(a) why the sum of two rational numbers is rational: suppose x,y are rational numbers. That means we can write x=a/b and y=c/d with integers a,b,c,d where b,d are non-zero. Then x+y = (ad+bc)/(bd). Since ad+bc and bd are integers and bd is not zero, we’ve shown that x+y is rational, which is what we wanted.
(b) why the sum of a rational number and an irrational number is irrational. Suppose y is rational, z is irrational and their sum is x=y+z. Then z=x-y=x + (-y). Since y is rational, so is -y, so we have expressed the irrational z as the sum of x and a rational number. By (a), if x were rational, then z would have to be rational too, which it isn’t, so x must be irrational.
(c) why the product of a rational number and an irrational number is irrational. As in (b), suppose y is a non-zero rational and z is irrational. Let x=yz be their product. Since y is not zero, we can write y=a/b with a and b both non-zero. Then z=(b/a)x is the product of x with a rational number. Since the product of two rational numbers is rational (easy proof), the hypothesis that x is rational would imply that z is irrational, so it must be rejected. Thus, x must be irrational.
I understand all of what you have indicated. I am not sure how we ask students to verify that they know or understand this. Is this standard to be addressed at a level where these proofs are reasonable expectations for students? The standard seems to be stated at a more introductory level which is what puzzles me regarding assessment.
Thank you for your response.
It’s a good question, Lisa. Because of the work of Deborah Ball and others, we have a good idea of what reasoning and proof can look like in elementary grades: students can explain why the sum of two odd numbers is even, for example, using visual representations of odd and even. In high school, we see geometry as a place where students learn to produce mathematical proofs. But Middle school has been a bit of wasteland for reasoning and proof. This standard provides an opportunity for that. One way of presenting Farshid’s argument to students might be to make the explicit connection with earlier understanding of the relationship between addition and subtraction, so that students can see that rational + irrational = rational would be the same as irrational = rational – rational, an impossibility. By the same token, rational times irrational = rational would be the same as irrational = rational/rational, also an impossibility. Then perhaps you could ask “by the way, how do we know that rational plus rational = rational?” This could be an opportunity to see the formula for fraction addition as not just a computational device, but as a fact about the system of rational numbers (that it is closed under addition).
There’s a danger that assessment will drive all this away, of course, attempting to reduce this standard to some mindless exercises; we have to resist that.
I agree Lisa’s question is a very important one, not just for this standard, but more globally in terms of “how do we engage students in reasoning and develop their ability to justify statements?” Back to this particular standard … Bill’s schematic explanation, cutting to the heart of the matter, is a good example of how a detailed explanation can look “starchy” and obscure the fundamental issue. Regarding getting middle and high school students to reason abstractly, when it comes to this particular standard, in my very limited experience with kids in this age group, what seems to fascinate them most about irrational numbers is that they are characterized by the fact that their decimal expansions don’t conclude with a recurring finite pattern. Perhaps the decimal expansion point of view on this standard can be a draw for some students? The question: “if you add a number whose decimal expansion has a repeating pattern to one that does not, what will happen?” is not straightforward and can generate a lot of good discussion among students.
1. Is the difference between the RI.4 standards (through grade 3) and the Language .6 standards that the reading standard ask students to conclude the definition of a word, while the language standards ask students to apply that knowledge?
RI.3.4. Determine the meaning of general academic and domain-specific words and phrases in a text relevant to a grade 3 topic or subject area.
L.3.6. Acquire and use accurately grade-appropriate conversational, general academic, and domain-specific words and phrases, including those that signal spatial and temporal relationships (e.g., After dinner that night we went looking for them).
2. How do RI.4 standards (grades 6-8) and the Language .5 standards differ? Both ask students to determine word meaning by connotation/denotation and of figurative language.
RI.8.4. Determine the meaning of words and phrases as they are used in a text, including figurative, connotative, and technical meanings; analyze the impact of specific word choices on meaning and tone, including analogies or allusions to other texts.
L.8.5. Demonstrate understanding of figurative language, word relationships, and nuances in word meanings.
Interpret figures of speech (e.g. verbal irony, puns) in context.
Use the relationship between particular words to better understand each of the words.
Distinguish among the connotations (associations) of words with similar denotations (definitions) (e.g., bullheaded, willful, firm, persistent, resolute).
Oops, guess I should have specified that I can only answer questions about the math standards!
1.OA.2 Solve word problems that call for addition of three whole numbers whose sum is less than or equal to 20, e.g., by using objects, drawings, and equations with a symbol for the unknown number to represent the problem.
Should the unknown be in all positions when dealing with addition of three whole numbers or only in the total?
The previous standard, 1.OA.1, about addition and subtraction word problems, requires the unknown in all positions, whereas this one leaves that open. It seems a natural interpretation to suppose that students can work on problems with the unknown can be in all positions for this standards as well, but that this is not a requirement for assessment purposes.
Bill,
Common vocabulary and definitions have been frequently-reoccurring requests. Many teachers are aware that there are different definitions for some mathematical terms (ex., trapezoid, isosceles, face). Similarly, there are questions about the appropriate language to introduce/use with students (either for developmental reasons, to better foster conceptual understanding, or to assure alignment with the coming tests). For example, should 5th grade students know and use the term “ordered pair,” or “coordinate pair,” both, or something else entirely?
This sort of grade-level specific “Suggested List of Mathematical Language” and “Math Glossary” were provided by our State Dept. of Ed. in the past. However, it doesn’t make sense for 45 states to produce different lists and different definitions for these “common” standards… especially if we will share common assessments. Is there any plan to provide this sort of supporting documents from groups you work with so that they are “common” for all 45 states? If not from your level, it seems very necessary that it be “common” at least within the PARCC states and within the SBAC states. Do they plan to produce such guidance documents?
Thanks,
Brian
Brian, this is a great idea, but I don’t know of any plan to organize it. Maybe you should start one! 🙂
Yes, I agree, Brian should start it, and I’m sure others like me would gladly help.
Bill,
There seems to be a bit of support out there for the idea. And I don’t mind working with my groups on producing first drafts. I have only two questions (and one request):
1. Is there a way to check with PARCC / SBAC that this work isn’t already in progress by their folks? (I’d be happy to send an email or make a phone call if you can send me the contact info. for someone who will actually give me an answer!)
2. If I coordinate an effort at drafts, would you (or any of your groups) be willing to look them over? If this sort of vetting is more appropriately done by some other group (ex., PARCC / SBAC or others), can you tell me who?
It would be hugely beneficial for the 45 states who have adopted if there was one “common” public space (ie., website) that was an “official” place to disseminate (
It doesn’t seem that there is any good mechanism in place to produce (or disseminate) this sort of inter-state infrastructure. Your blog and the Illustrative Math Project are the closest we have. As a result, 45 states are duplicating efforts and producing different interpretations of the “common” standards. Is there any way to get one “official” website that would function as a *common* public space to house *common* resources for the 45 states and have *common* inter-state discussions? Please?!
I know that a lot this comes down to funding… but it seems like individual states have been given a LOT of RTT money that could go a lot farther (and we could reduce the risk of splintering the common standards) if work could be done once by a group of inter-state folks and then shared on ONE inter-state space!
Thank you for sharing your thoughts, answers, and providing this blog as a common space,
Brian
One of ther question that I would have is… has anyone taken a poll of the CC states to see which states have adopted the Traditional Model at the HS level vs. the Integrated approach? This could be useful as we begin to share information/resources, etc. Thank you.
This would be a fantastic resource for our districts/teachers as one of the larger issues that I see with our math instruction in our area is a lack of vertical alignment (both in instruction and in terminology/definitions). Like many of you, our districts will be re-working curriculum maps that align with the Common Core language/content.
I agree with Brian that this would be very useful. It would be nice for teachers to have common definitions and a common list of key terms to focus on. It would be helpful to see the terms taught in the grades prior to you that are fair game and which terms are introduced after your grade level. I would be willing to help with this if anyone else is interested on working on this. How can we make sure that what is created is connected to the assessment creation process. It wouldn’t do much good to give teachers a list of what we think should be taught at each level and then have the test creators working with a different set of vocabulary terms.
I, too, agree that it doesn’t make a whole lot of sense for the CCSS states to be duplicating efforts left and right!! I know that there is a mapping project for the ELA CCSS (There’s a fee, I believe!) and the same group has indicated the possibility of beginning a mapping project for math. In the meantime, The Dana Center (funny that it’s out of Texas!) has a scope and sequence available for use for CCSS in math. Early elementary teachers, check out Winnipeg School Division Numeracy Project; I think some of the ideas/activities are great foe CCSS!!
Both PARCC and Smarter Balanced indicate a classification system for the content clusters as “major, supporting, and additional.” Do you know where that comes from, or who did that, and is it in line with the original intent of the standards?
These are products of the consortia themselves, in their efforts to ensure that the assessments focus on the key ideas in each grade. I haven’t done a thorough or detailed analysis, but I’ve read through them and by and large I would say that yes, they capture the focus in the standards.
I teach HS Math (specifically Algebra 2). How do you envision how math class would be taught with the Common Core Standards? I think many teachers teach math in a fairly “traditional” way – instructing students on how to do (whatever) and then assign problems to be completed. How is our “mode of business,” if you will, going to change?
Thanks – Lisa
Dear Lisa, I don’t see the standards as dictating any particular teaching method, but rather setting goals for student understanding. Different people have different ideas about what is the best method for achieving that understanding. That said, I think it’s pretty clear that classrooms implementing the standards should have some way of fostering understanding and reasoning, and classrooms where students are just sitting and listening are unlikely to achieve that.
I have a question about the statistics component in Algebra 2. How are students going to be expected to determine margins of error by simulation? Also, exactly why is this being done in this course, when more direct, classical methods for confidence intervals and hypothesis tests are discussed in AP Staistics?
Primary teachers become very emotional about the placement of the time and money standards. Kindergarten- no standards on time or money; Grade 1-telling and writing time, no money standards; Grade 2-time and money; Grade 3-no money standards. I have shared my view and would like to share your response which I am certain has more credibitlity.
Reading time and knowing the value of coins are important life skills, which students could learn in many places: in the home, in social studies, in science, in mathematics, in history, or in english language arts. There has been a tendency to overload mathematics standards in particular with these life skills, at the expense of more important work on number and operations. Perhaps this was because mathematics standards came along first, so putting these things there was a way of ensuring they were taught. The view of the Common Core is that, used in the right way, they can be tools for learning about number and operations, but they are not mathematics topics in their own right. If kids come to school with knowledge about them, or if there is a way of weaving them into the curriculum that supports the main focus, then that’s fine. But too often they become the main focus themselves. The strongest message of the Common Core is: focus on what’s important and give it the time it needs, so that kids have a chance to learn it well and progress onto other things. That required paring down previous standards.
I interpret your comment to mean that the using money to practice counting by 1’s, 10’s, and 5’s in their respective levels or using the clock to practice numeral identification would be reasonable, as those are real-life applications of the mathematics students are expected to be exploring at their level. However, pushing students to count with mixed coins before they have a sense of number composition and decomposition would be discouraged.
Hi Bill,
I am used to there being preliminary work with similar figures in Grade 7 after working with proportions. However, it seems that the intent of the standards is to introduce congruence and similarity with transformations in Grade 8. If this is the case, could you explain the benefit of this approach being taken in the standards?
Thank you for taking the time to answer our questions.
Monique, the Grade 7 standards 7.G.1 gets at some of what you want here: “Solve problems involving scale drawings of geometric figures, including computing actual lengths and areas from a scale drawing and reproducing a scale drawing at a different scale.” It gives an opportunity for student to play around with the informal notion of similarity, without calling it that. There’s a mathematical problem with teaching similarity before congruence, in that the notion of similarity depends on the notion of congruency. That is, two figures are similar if you can scale one so that it is congruent to the other. So that’s the reason for introducing the formal notion of similarity after congruence.
Again, looking for some guidance — first, I noticed that the progressions for High School Stats is soon to be released. I look forward to that. I am currently studying S-CP.5. It clearly says “in everyday language”. Does this mean that we want students to simply reason about the independence of events.
While I understand what this is saying I am not sure how we assess students in a fair and consistent manner on standards such as this. In everyday language seems to imply that some outside knowledge will be required to discuss these types of situations. Is there a possible sample item that is nearly ready for the illustrative math site that could shed some light on this standard?
Lisa, we don’t have anything in the task bank for S-CP.5 yet, probably because you are right, it’s hard to assess. This standard might be best assessed with a modeling task, where students are expected to choose a model for a situation, including making assumptions about whether events are independent or not, and then evaluating their assumptions. We have a few modeling tasks up on Illustrative Math, but not yet for this standard. If you have any ideas for a task, let me know!
Hello.
I tried to find the standard associated with simplifying fractions in the lowest terms. However, I couldn’t. Can you explain when teachers teach this skill to which grade students?
Kim, the Standards do not require simplifying fractions into lowest terms, since it is not a mathematically important topic. To quote the Fractions Progression , “It is possible to over-emphasise the importance of reducing fractions …. There is no mathematical reason why fractions must be written in reduced form, although it may be convenient to do so in simple cases.”
Indeed, there are situations where simplifying fractions gets in the way of understanding. For example, insisting that the answer to 1/10 + 3/10 be written as 2/5 gets in the way of the most important understanding that we want students to come away from this problem with, namely that this addition works the same way as whole number addition, with the unit 1 being replaced by the unit 1/10.
I have a question about line plots/dot plots. Are they used exclusively for measurement data? I see that they are mentioned as the vehicle for displaying and analyzing measurement data in the progressions document, but I wasn’t sure if this meant that you should not use them to represent categorical data. Thanks!
Yes, these are for measurement data. The number of dots above a given measurement on the horizontal scale indicates how many times that measurement occurs in the data set. When you do the same sort of thing with categorical data you would call it a bar graph.
Hi Bill,
Thanks for the opportunity to ask questions for you and the community. I looked for simplyfing radicals as an individual learning standard and was unable to find it. Is this purposeful have I overlooked this skill? 8.EE is close and so is N.RN.2 . Is this like the above conversation about simplifying fractions?
I apologize, Bill has already replied to this topic on another post chain, here’s his answer:
“The standard N-RN.2, Rewrite expressions involving radicals and rational exponents using the properties of exponents, could support some work along these lines. But the standards overall try to get away from demanding that students “simplify” things. For example, they don’t expect students to find the least common denominator when adding fractions, or to reduce fractions to lowest terms. When thinking about radicals, it’s not at all obvious that 3 \sqrt{3} is simpler than \sqrt{27}, and the latter form is more useful for some purposes. For example, you can see that the number is slightly bigger than 5 much more easily from this form.”
Thanks, sorry for the oversight.
No worries, I had forgotten about that post. Nice to see that I am consistent.
You’ve got the right standards there, particularly N-RN.2. I would also include A-SSE.3. Students should be able to rewrite $\sqrt{12}$ as $2 \sqrt{3}$ and vice versa, but neither of these is simpler than the other. The emphasis in the standards is on transforming expressions into different forms for a particular purpose, as described in A-SSE.3. So yes, it’s similar to the conversation about fractions. The word “simplify” does not occur in the standards (except in one grade level introduction, which was an editing error).
That’s a great idea about “simplify” not being simpler! One of the biggest hurdles for Algebra 2 students, though, is working with rational expressions/equations when they are inexperienced with finding that least common denominator. They want to multiply all the denominators together and end up with 4th and 5th power polynomials in the numerator instead of easily factorable quadratics. How do the successful countries handle a problem like that? Do they skip the least common denominator or is it something we are overlooking?
Regarding 8.G.3: When using coordinates to show the effects of transformations should students be able to extend that knowledge to rotation and dilation points other than the origin? It seems that distance from the origin is the basis so I was wondering if they should be able to extend that knowledge.
Well, you can have a rotation about any point and a dilation from any point, so I guess those would be included. Note that in 8.G.8 students are using the Pythagorean theorem to calculate the distance between any two points.
Hi Bill,
The progressions document on Ratios and Proportional Reasoning 6-7 has been incredibly helpful as I attempt to dig into 6.RP.3a-d. However, I have two questions about 6.RP.3d:
1) I’m not sure I understand the expectation for students where it states, “manipulate and transform units”. The standard is clear up to that point, but this phrase seems to suggest actions other than converting. Am I trying to read too much into it? Or is this suggesting some application of the standards for mathematical practice that I am not seeing?
2) From the last paragraph on p. 7 of the progressions document, it seems that converting units between measurement systems (customary to metric and vice versa) using ratio reasoning is an expectation for sixth graders. Is this correct?
1) It could mean also understanding that when you multiply a quantity expressed in seconds by a quantity expressed in meters per second, then you get a quantity expressed in meters. Also dealing with things like minutes times meters/second, or feet times acres (connecting with 6.G.2).
2) Well, the progression suggests it as a possibility for 6.RP.3d, not a requirement. It’s a natural thing to do, but the standard does not give an explicit list of which unit conversions are expected, so there is room for curriculum writers to use their judgment here.
Thanks so much for taking time to repond to all of these questions. What it meant when in third grade NF 3 special cases?
3NF3. Explain equivalence of fractions in special cases, and compare fractions by reasoning about their size.
Not sure what “special cases” may be, but the denominators in Grade 3 are limited to 2, 3, 4, 6, and 8. Although the CCSS does not limit the fractions to be discussed in Grade 3 to proper fractions, there are still infinitely many fractions with those denominators. However, I would suspect that the limit of equivalent fractions in Grade 3 will be basically the proper fraction situations, that is, 1/2 = 2/4 = 3/6 = 4/8, 1/3 = 2/6, 2/3 = 4/6, 1/4 = 2/8 and 3/4 = 6/8.
Tad has it right. The idea is to limit to situations where you can see the equivalence by direct reasoning from the definition of a fraction, but not get into the general way of seeing equivalence. For example, you might see that 1/2 is equivalent to 3/6 using a tape diagram divided into 2 and then into 6. But you wouldn’t get into 3/6 = 3×1/3×2 = 1/2.
Bill,
We are eagerly awaiting the release of the Geometry Learning Progressions and the measurement part of the Measurement and Data Learning Progressions. As we’re analyzing 3.MD.2 and 4.MD.2, we’re wondering about instruction related to “masses of objects” with elementary school students. Since elementary students typically focus on objects on Earth, the distinction between mass and weight is not emphasized in most elementary classrooms, and many elementary school teachers often use the terms mass and weight interchangeably. However, we don’t see any references to weight in the CCSS (other than K.MD.1-2), and we don’t want teachers to inadvertantly foster misconceptions. Should we follow the more technical route and ONLY refer to “mass” when measuring or estimating with g and kg? Or, is it okay to meet students where they are and allow teachers to use “weight” (or to interchangeably use mass/weight) since weight is more commonly used in authentic contexts. Your insight would be greatly appreciated. Thank you in advance.
This seems to me a case where the judgement of the teacher or curriculum writer is important. On the one hand, there are opportunities to model correct usage here (e.g., talking about the mass of the earth). On the other hand, you don’t want to forbid people from using common language such as “I weigh 60 kg”.
As teachers and curriculum writers exercise this judgment, I hope they turn to Mathematical Practice 6 (Attend to Precision) for some guidance. It seems to me that there is nothing incorrect about measuring mass in pounds (though it is definitely not conventional). “Weight” is measured on a scale and is affected by gravity. “Mass” is measured on a balance, which means that changing gravitational pulls would not affect it. For example, my weight on earth would be different than my weight on the moon; however, my mass would be the same on earth as on the moon.
With this, it seems that using mass and weight interchangeably would not be ‘Attending to Precision,’ as they are not synonymous. I would not have a problem using pounds as a unit for measuring mass, as long as we are measuring on a balance.
Thanks for doing this, Bill! I see a big emphasis on equations, tables, and graphs that represent proportional relationships in the standards, and I am wondering where the first place is that you might introduce an algebraic relationship between variables that is not proportional (e.g. y = mx +b where b is non-zero). Is that something to be included in 6.EE.9 (Use variables to represent two quantities in a real-world problem that change in relationship to one another) or is it something that first appears in 8th grade Functions or somewhere in between?
Clarification: I see where solving equations of the form falls, but I am wondering about relationships between variables that change, that you might graph on a coordinate plane.
I think this is certainly something that could be included 6.EE.9.
In your post on Arranging the High School Standards into Courses, you lay out a 159 day pacing guide for Algebra I. In California, the state testing window opens about 145 days into the school year. Plus, there are many interruptions that take instructional days away. What would you recommend if we were trying to build a 130 day blueprint?
Mark and Bill,
This is very similar to that of New York State with the number of days that teachers have to teach. The 130 day layout would be beneficial (although I would assume that with only 130 days, it would make sense to “borrow” the days from all of the areas). What also interests me is building this kind of a pacing guide with SLO’s and Interim assessments scattered throughout. We are pushing for at least three Interims throughout the year. We would also need to build in some time for the scoring of the interims and SLO’s (espcially SLO’s given that teachers who have a stake in student achievement should not grade their own students’ papers… which leads to regional scoring).
Anyone else thinking about this as well?
Mark –
You mention state testing (CSTs). In high school, the Common Core State Standards will not be tested with CST End of Course Exams. The summative assessment in high school (CA is part of SMARTER Balanced Assessment Consortium) will be at the end of junior year, and all standards except those marked with a (+) can be tested. Our current testing model will be different, with schools and districts having some flexibility over the testing window in the 11th grade.
Also from NY…. Sounds like you’re talking 4-8 testing and not Regents. SLO’s will be used for those subjects who don’t have CCSS. NY has joined PARCC (but not adopted the assessments, yet, hence the pilot questions on this year’s state tests as a back-up in case PARCC on-line isn’t ready for next year!) They are also looking at the major assessment being given at about 90% completion of the year’s instruction and are backing off of quarterly assessment being ready for delivery in 2012-2013.
I work with high school mathematics teachers and would like to ask a question though I’m sure others will follow as we continue to decompose what is within the standards. I do not see any direct mention of the angles of polygons within the CCSS. Of course, there is G.SRT.5 Use congruence and similarity criteria for triangles to solve problems and to prove relationships in geometric figures. We can easily see how angles of polygons could be included in this standard as well as more generalized ideas. Would you clarify this for us?
Kaycie,
Maybe what you are looking for is included in 8.G.5 (Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles. For example, arrange three copies of the same triangle so that the sum of the three angles appears to form a line, and give an argument in terms of transversals why this is so.)?
Brian
I agree that this standard from eighth grade will be the beginning place for the conversation regarding interior and exterior angles of polygons by concentrating on triangles, but it does not seem to give rise to other polygons with n sides where n is greater than or equal to 3.
I was wondering about this also. My interpretation is that it is appropriate to informally explore the angle sum rule for an n-sided polygon in 8th grade using triangles, potentially having students make a conjecture about a formula. However, formal teaching of it does not seem required nor forbidden in 8th grade. Perhaps a future high school geometry progression document will “shed light on the problem.”
Monique is correct: there are opportunities in the standards to explore the angle sum formula for polygons, but it is not explicitly required.
What does it mean to “prove that, given a system of two equations in two variables, replacing one equation by the sum of that equation and a multiple of the other produces a system with the same solutions.” (A.REI.5) Does that mean a formalized proof of some type – algebraic or by argument or flow chart or what? Our teachers know how to present solving systems of equations by linear combination easily enough and how to have students demonstrate their understanding of that skill, but they are stumped by what is expected of students with a proof that linear combinations provides the same solution to the original system of equations.
Any insights you can provide will be greatly appreciated.
The proof does not have to be a standalone formal object, it could well be embedded in a presentation of the method. There’s a difference between showing how to use a method and explaining why it works. I think it’s a question of the language used while presenting the method. For example, you might say that if (a,b) is a solutions tp a system, then the left side of each equation is equal to the right side of each equation, so adding the left sides gives the same number as adding the right sides. That’s a bit different from just showing the mechanics of adding the equations.
Bill,
My wife and I are teaching elementary school teachers the principles of Common Core Math in the lower grades. As part of these courses, we give teachers a syllabus with links to relevant material on the internet. You have provided invaluable illustrations of every standard and I would love to provide a link for the teachers to supplement many of the standards being taught (for example: “3.NF Locating Fractions Greater than One on the Number Line”. However I have not found a simple way of linking to specific discussions and illustrations. We give the teachers the general URL (http://illustrativemathematics.org/standards/k8) to the content standards and tell them the detailed path for finding a particular discussion or illustration. My bet is that most are not willing to follow these fairly tedious paths.
Is there any way to link to this material without going to home page and using the cascading menus?
A related question is whether there would be any problem if I copied the text and illustrations of interest and put it in the syllabus.
Robert Springer
We will have the ability to link to tasks soon. As for the copying question, it’s fine as long as you acknowledge the source, and follow the rules in the license (bottom left of the page).
Hi Robert,
I just wanted to follow up and let you know that the ability to directly link to a task at illustrativemathematics.org is now available. We are also working on providing a pdf link for all tasks, but that is a work in progress for older tasks.
Cheers,
Ashli
Dr. McCallum,
I need help with clarifying the fluency with addition and subtraction facts in K-2.
K- Fluent with addition & subtraction w/in 5
1- Fluent with addition & subtraction w/in 10
2- Fluent with addition & subtraction w/in 20 AND knows from memory single-digit to 9+9 (add only)
We are working on standards based report cards for our 1-2 grade levels. We have standards based in Kinder already. This year in kinder, we listed the standard as shown and then, for assessment purposes only, we used flash cards to assess fluency. (We were sure to use number talks, images, and manipulatives to ensure understanding).
When we started working on standards based for 1 and 2 we ran into some confusion, because we had at first thought in K and 1 we should be “flash card fluent” under 5 and under 10 respectively, but then in 2nd it says know from memory for the ones they should be “flash card fluent” with and the word fluent has a slightly different meaning.
What wording could be used on a report card to differentiate these skills for parents? And if the K and 1 should not be “know from memory” how should teachers assess the facts in kinder and first?
In November 2000 issue of Teaching Children Mathematics, Susan Jo Russell discussed what NCTM meant by “fluency.” She writes (p. 154):
—
Fluency, as used in Principles and Standards, includes three ideas: efficiency, accuracy, and flexibility.
• Efficiency implies that the student does not get bogged down in many steps or lose track of the logic of the strategy. An efficient strategy is one that the student can carry out easily, keeping track of subproblems and making use of inter- mediate results to solve the problem.
• Accuracy depends on several aspects of the problem-solving process, among them, careful recording, the knowledge of basic number com- binations and other important number relation- ships, and concern for double-checking results.
• Flexibility requires the knowledge of more than one approach to solving a particular kind of problem. Students need to be flexible to be able to choose an appropriate strategy for the prob- lem at hand and also to use one method to solve a problem and another method to double-check the results.
—
I don’t know if this view is consistent with the CCSS writers’ view, but I like (yes, my personal preference) this view on fluency. It should also be noted that “fluency” seen from this perspective does not necessarily mean “quick.”
I also think it is interesting that the CCSS distinguish “fluency within 20” and “knows from memory ” up to 9+9. This seems to suggest that students should be fluent with calculations like 13+5 and 18-3 using their understanding of the meaning of operations and number sense. But, for 1+1 … 9+9, the CCSS seems to expect students to “just know” the facts. I also like the fact that the CCSS puts “memorization” AFTER fluency. I think if students become fluent (as explained by Russell), they will remember basic facts, too.
Thanks Tad. So in your opinion, would you start assesessing “know from memory” addition facts only in kinder under 5 and under 10 in 1st as a progression toward the 2nd grade standard?
Or would you just expect them to be able to do them “unhaltingly” but not necessarily from memory?
For our second graders we are using flash cards to assess during individual student interviews and we expect them to know the fact within 3 seconds. Thoughts?
First, “fluently” refers to how you do a calculation, whereas “know from memory” means being able to produce the answer when prompted without having to do a calculation. In CCSS, “fluent” means “fast and accurate.” The sort of flexibility that Tad is talking about is coded into many of the standards that are not explicitly about fluency, so it is part of the standards as a whole. I note that Tad says “fluent” does not necessarily imply “quick”, whereas I have said that it does imply “fast”. So there seems to be a bit of disagreement there, although maybe not that much; “fast” for a Kindergartner is not as fast as “fast” for a 2nd grader. If a Kindergartner adds numbers within 5 by saying the starting number and then counting on at a normal verbal pace, without hesitation, and gets it right each time, then I would say the student is fluently adding within 5.
I think it is a matter of how quick is quick enough. For example, in Grade 1, if a child thinks, without hesitation, “9 + 4 is 9 and 1 is 10 and 3 more is 13” it will be quick enough to be fluent. However, it is definitely not as quick as simply recalling the fact 9+4=13.
On the other hand, Russell’s definition of fluency may be a bit problematic. For example, if a 2nd grader is adding 9 + 8 by counting on 8 times from 9, without hesitation, is he fluent? I would say no because I would want 2nd graders to be moving away from inefficient counting strategy to obtain the correct answer.
As for assessing Kindergarteners, my inclination is not to worry about “know from memory” since the CCSS does not say it explicitly. I may still use flash cards to pose questions, but I would be assessing not how quickly students give me the correct answers but how they seem to be obtaining the answers.
Okay, I would start this post with “one more question” but I can’t guarantee it will be my last. 🙂
K.G.5 Model shapes in the world by building shapes from components (e.g., sticks and clay balls) and drawing shapes.
Is this referring to both 2-D and 3-D shapes, and which shapes should we expect them to model as opposed to draw and vice versa?
I think both “building” and “drawing” are types of “modeling.” So, it’s not a matter of whether students should model or draw.
Modeling (drawing and building) with different materials allow Kindergarten students to start paying attention to the parts that make up shapes. So, students should engage in modeling activities using tiles (pre-made shapes), sticks (focusing on sides of polygons), drawing by connecting dots on dot grid (seeing the vertices of polygons), etc.. Kindergarteners don’t have to specify those components by formal terms, but those experiences help them move from just seeing the whole shape to being able to (eventually) analyze the components of shapes.
CCSS seems to put a lot more emphasis on 3-D shapes, so I imagine students should have some experiences with building 3-D shapes (with blocks, empty boxes, sticks and clay balls, etc.). But, drawing, i.e., representing 3-D shapes on a 2-D medium is probably too much for Kindergarteners.
1.G.2 Compose two-dimensional shapes or three dimensional shapes to create a composite shape, and compse new shapes from the composite shape.
The second part of this standard confuses me. What exactly does that entail?
I believe I understand the first portion as combining two right triangles to make a square, which would be your “composite” shape. So would you take the new square (the composite shape) and another square to make a rectangle? (Obviously this is just one example.)
p.s. Love this blog. Really looking forward to the progressions in Geometry!
Yes, your example certainly fits the standard. Also, situations where you use those interlocking cubes to build up lines, then put the lines together to make rectangles. One of the purposes of this is to get students accustomed to holding more than two different levels of structure in their minds.
Can someone clarify F.LE.1a? “Prove that linear functions grow by equal differences over equal intervals; and that exponential functions grow by equal factors over equal intervals”. Do the students need to be able to do a formal proof of this? Or will they be given an example and they have to justify it?
I think it’s somewhere in between formal proof and giving an example. I can imagine a lesson that starts with examples, and then asks students to “look for and express regularity in repeated reasoning” (MP8) and come up with a general algebraic argument. That argument could look something like this: if f(x) = mx + b, then f(x) grows by mh over any interval of length h, because f(x+h) – f(x) = m(x+h) + b – mx – b = mh. Initially students might just look at cases where the length of the interval is 1, and where m and b are given numbers, and then build up from there.
This looks like a precursor for the definition of a derivative…from a a typical 13- or 14-year old Algebra I student. I’m biting my lip on this one. Our 17- 18- year- old AP Calc students find that definition challenging to wrap their minds around when it is given to them. Is there something I’m misinterpreting here as far as expectations for Algebra I?
Could someone provide clarification on A.REI.7: “Solve a simple system consisting of a linear equation and a quadratic equation in two variables algebraically and graphically.” What is the definition of a quadratic used here? Does it include circles, elipses, hyperbolas? Or just parabolas?
Examples involving circles, ellipses, and hyperbolas certainly fit with the standard. However, the standard does not require that you cover all of these cases.
Our district is looking for clarification on: A.CED.2: “Create equations in two or more variables to represent relationships between quantities; Graph equations on coordinate axes with labels and scales.” When this strand refers to “two or more variables” does that infer that we need to solve equations with three variables? Would this include teaching matrices?
Note that this standard is not about solving equations, but about writing them. It does not include matrices. For example, it includes writing the equation Q = 100 + 5t to represent a quantity that grows at a constant rate, and then graphing Q against t. The “two or more variables” allows for situations where you might have a quantity that depends on more than one variable. For example, the balance in a bank account might depend on both the number of years t and on the interest rate r, B = 1000(1+r)^t.
Our department has been trying to interpret the strands and we are having a difficult time. One question we have is regarding N.Q.3. (Choose a level of accuracy appropriate to limitations on measurement when reporting quantities). Does this mean that students should be able to calculate relative error and percent error?
No, that exceeds the standard. The standard just mean students should be able to choose the right level of accuracy. For example, if the legs of a right triangle are measured using a ruler marked in 10ths of a centimeter, and you calculate the hypotenuse using the Pythagorean theorem, it does not make sense to report the answer to two decimal places.
Would teaching rules for computing with significant figures also exceed the standard? Science teachers would be pleased if such rules were taught in first-year algebra.
I too have the same question and am interested to know the response to the question David referred to below on April 30, 2012. Please let us know.
I’m trying to understand the placement of this standard N-RN.3 in Unit 5 (Appendix A) and what the teaching of it entails in the context of the Unit. It appears nowhere else in any course. I’m thinking it may be pointing to understanding and working with radicals since radicals consistently appear while working with quadratics. If it is pointing to radicals, why was it not introduced in Unit 4 when students are working with quadratic expressions and equations?
I agree it sticks out where it is. I see Appendix A as a first attempt at arranging the high school standards into courses, and there are no doubt many opportunities for people to come up with better ideas. This standard is really a capstone for work on the number system from earlier grades.
has anyone developed potential timelines for teaching with the common core standards? Our district is finding it difficult to get through all the topics in time for state tests which occur in April.
Hi Scott,
This post might be what you are looking for: http://commoncoretools.me/2012/03/16/arranging-the-high-school-standards-into-courses/
Cheers,
Ashli
Has anyone published potential timelines for grades K-8? I just produced my first draft of a timeline for 7th grade. I would like to compare it to some others before I start using it in September.
In our county-wide meetings, multiple districts have collaborated to cluster standards together into a sequence of units of instruction, using the PARCC frameworks and the progression documents as a guide. I can send them to you if you’d like. Email me at jwinters@lake.k12.il.us.
Connecticut has done some work with creating units for grades K-8. This may be helpful for you. There is a section on this page called Illustrated practices, units and pacing guides.
http://commoncore.greenwich.wikispaces.net/math+resources
Their work states that is was adapted from the Arizona Dept of Education
http://www.azed.gov/standards-practices/mathematics-standards/
Can you clarify if “A-REI 3. Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.”
includes the expectation of using a linear equation to solve an exponential equation in Algebra I/Math I?
In Appendix A it states: Extend earlier work with solving linear equations to solving linear inequalities in one variable and to solving literal equations that are linear in the variable being solved for. Include simple exponential equations that rely only on application of the laws of exponents, such as 5x = 125 or 2x = 1/16 .
A-REI.3 itself is silent on the arrangement of topics into courses, so it can’t by itself be interpreted as saying which types of equations occur in Algebra I/Math I and which occur later. Appendix A is a sample arrangement of the standards into courses, but it does not carry the force of the standards themselves; that is to say, a curriculum can follow the standards without following Appendix A. I’m not sure exactly what you mean by “using a linear equation to solve an exponential equation”. The example you quote from Appendix A is about understanding the laws of exponents, not about linear equations.
Hello!
I have a question about mode in the CC. I see median and mean mentioned in grade 6, but no mention of mode. Where should mode come into play, if at all?
Thanks so much for all of your insights. Excellent blog!
Bridgett,
The usefulness of mode is dependent on the nature of the data. If a data set is discrete with a small number of different values, e.g. how many pets each of our students own, then the mode may have significance. If it tends to be more continuous and/or have a lot of different values, e.g. the heights of our students measured in cm, then the mode may not tell us anything useful.
6.SP.5d asks students to relate the choice of measure of center to shape and context. That gets to the root of it. If mode is part of a curriculum, there should be conceptual understanding of what it does and doesn’t) tell us about our data, beyond the skill of computing it.
Bridgett,
The usefulness of the mode depends on the nature of the data. If the data are discrete with a limited number of values (e.g. the number of pets each of our students own), then the mode may tell us something interesting. If the data are more continuous with many different valued (e.g. the heights of our students measured in cm), then the mode may be of little use.
6.SP.5d speaks of relating choice of measure of center to shape and context. That is the heart of it. Students should understand conceptually when the mode is and is not useful as a summary measure.
Bridgett, you are correct that knowing about the mode is not a requirement of the standards. An important design principle for the standards was focus, which meant eliminating topics of secondary importance to provide more time to cover the remaining topics in depth.
Bill,
First, thank you for answering all of our questions posted here. My questions are regarding Geometry in Grade 5.
5.G.3 Understand that attributes belonging to a category of two-dimensional figures also belong to all subcategories of that category. For example, all rectangles have four right angles and squares are rectangles, so all squares have four right angles.
5.G.4 Classify two-dimensional figures in a hierarchy based on properties.
– How detailed should the hierarchy of 2-dimensional shapes be? Should kite be included?
– Also, what is the definition of a trapezoid? Is it “only one” pair of parallel sides or “at least” one pair of parallel sides? This would affect the hierarchy diagram.
Note: According to Van de Walle (2010) in Elementary and Middle School Mathematics, 7th Ed., “Some definitions of trapezoids specify only one pair of parallel sides, in which case the parallelogram would not be a trapezoid. The University of Chicago School Mathematics Project (UCSMP) uses the “at least one pair” definition, meaning that parallelograms and rectangles are trapezoids” (p. 411).
Thanks,
Trish
I am very curious to know the answer to the trapezoid definition question. However, in the final report of the National Math Panel, you find this statement:
“By the end of Grade 5, students should be able to solve problems involving perimeter and area of triangles and all quadrilaterals having at least one pair of parallel sides (i.e., trapezoids).” (p. 20)
So, it appears that the NMP is saying that the definition of trapezoids is “at least” one pair of parallel sides.
The trapezoid issue has come up in our county before. The way I deal with the possibility of having two distinct definitions is by making the students and teachers aware that some people agree on “only one pair” whereas some people agree on “at least one pair” of parallel sides. I leave it open to discussion. Often times people say they like math because there is always a “correct answer.” But this is not always true. This is one case where discussion and understanding of other opinions is essential.
Our state (Florida) defined trapezoids in our testing glossary. So though we had great discussions, we let the students know that ultimately on our state test, we will define trapezoids as having only one pair of parallel lines. I imagine more clarity will come with test item specification from either PARCC or SBAC.
Thanks for your patience while I catch up on answers to these questions. This discussion as already laid out the issues pretty well. The fact is that there are two competing definitions out there, and no authority (including CCSS) says which one to use. That said, I think there are good mathematical reasons for choosing inclusive definitions (e.g., a rectangle is a trapezoid, a square is a rectangle). It’s hard to imagine a situation where you want to state a property of a trapezoid that depends on one pair of sides not being parallel, so in practice what you say about trapezoids will be true of parallelograms as well. It’s awkward to have to keep saying “and this is also true of parallelograms” every time you make a statement.
The inclusive language also inspires connection between formulas. Since the trapazoid’s area is the average of the bases times the height, then we could say the same for a parallelogram. If students can “see” so many of the formulas as simple variations of bh (or Bh for volume), there is less to memorize.
Usiskin et al.’s Classification of Quadrilaterals reports on the results of a systematic survey of textbooks and has a discussion that some might find helpful. You can see it via Google Books: http://books.google.com/books?id=ZkoUR5lRwdcC&lpg=PA32&ots=WKi19q9x61&dq=whiteley%202002%20trapezoid&pg=PA32#v=onepage&q&f=false
Usiskin et al. say: “The preponderance of advantages to the inclusive definition of trapezoid has caused all the articles we could find on the subject, and most college-bound geometry books, to favor the inclusive definition.”
3.OA.7 Fluently multiply and divide within 100 and know from memory all basic facts up to 9×9.
In addition to knowing from memory the basic multiplication facts are 3rd graders becoming fluent with 2-digit by 1 -digit multiplication so long as the product is 100 or less? For example they should be expected to find 27 x 3 or 15 x 4, but not 47 x 5 or 85 x 2.
Leandra,
I don’t think that is the intention of the standard. I believe they just used the “within 100” example to cover all of the possible products of one digit factors. In fact, looking in 3.OA.7 it does say products of two one digit numbers.
Joe, so in your opinion there is no double digit multiplication in 3rd grade except by multiples o ten? Or am I maybe missing it in another standard?
Multiplication of 1-digit by 2-digit numbers is included as long as the product is less than 100. From the glossary (on page 85 of the standards):
Multiplication and division within 100. Multiplication or division of two whole numbers with whole number answers, and with product or dividend in the range 0-100. Example: 72 ÷ 8 = 9.
3.OA.7
Multiply and divide within 100.
7. Fluently multiply and divide within 100, using strategies such as the
relationship between multiplication and division (e.g., knowing that 8 ×
5 = 40, one knows 40 ÷ 5 = 8) or properties of operations. By the end
of Grade 3, know from memory all products of two one-digit numbers.
So Bill, in looking at the glossary, the standard and your post, it sounds as if this is an issue where the standard is not limiting, but stating the minimum we should expose our students to and hold them accountable for. We could go beyond. For instance, they should leave 3rd grade with a working knowledge of all products from two one-digit numbers, but they may also be exposed to working with products of a one-digit and two-digit number within 100. The glossary doesn’t seem to define for us what IS included, nor does it tell us what is NOT included. This is another issue where the standard is very open to interpretation. Also in looking at 4th grade standard 4.NBT.5, that is a standard that does specifically mention multiplication with a one-digit by a multi-digit number, which the 3rd grade standard does not do.
I’m making this reply after I have already posted my reply below:
One thing that does seem contradictory to the statement of multiplying withing products of 100 is 3.NBT.3, multiply one-digit numbers by multiples of 10 in the range 10-90. Even one example listed in the progression document (K-5 Number and Operations in Base Ten) shows 3 groups of 50, which would of course result in a product greater than 100.
My interpretation then would be that for students to explore equal groups of two-digit numbers is expected in third grade. Which makes sense when students are learning conceptually of what the meaning of multiplication is, as well as using place value throughout operations. (Modeling 3 groups of 25 would not be that different conceptually than modeling 6 groups of 4.) But for fluency, third graders would be expected to learn related multiplication and division facts of one-digit by one-digit factors.
I have been following this 3rd grade thread and hoping that there would be additional clarification on division. The AZ standards and practices use a model of 92 divided by 4 (4 students sharing 94 objects). Does this continue the same skill/conceptual standard as “Multiplication of 1-digit by 2-digit numbers is included as long as the product is less than 100. From the glossary (on page 85 of the standards)”?
Any dividend less than 100 is acceptable for 3rd grade division????
Yes the standard says multiplication AND DIVISION within 100. The glossary then defines that as having a product OR DIVIDEND within the range of 0-100. The only stipulation here is no remainders. I missed the glossary before I posted my question. 🙂
I am wondering about the difference between 6.NS.8 (Solve real-world and mathematical problems by graphing points in all four quadrants of the coordinate plane. Include use of coordinates and absolute value to find distances between points with the same first coordinate or the same second coordinate.) and 6.G.3 (Draw polygons in the coordinate plane given coordinates for the vertices; use coordinates to find the length of a side joining points with the same first coordinate or the same second coordinate. Apply these techniques in the context of solving real-world and mathematical problems.)
I see that 6.NS.8 could be interpreted much more broadly than 6.G.3, so I guess I am wondering what are appropriate 6.NS.8-type tasks that are NOT already 6.G.3-type tasks? I would not include graphing proportional relationships or relationships between an independent and a dependent variable as there are other standards about those situations.
I checked illustratedmathematics.org and didn’t find any illustrations for these. Looking forward to having some soon! All of this has been so helpful!
Liz, thanks for pointing this out, I’ll let the Illustrative Mathematics team know!
I’m wondering why I don’t see as much “push” for CCSS math as there is for English-Literacy when so many more students require remedial math than reading when entering college. Is this just in Missouri?
No, Lane, it seems to be that way in NY too. So I don’t think it’s just Missouri. Many of our RTTT state sponsored training sessions have been on ELA, and we have had minimal training on the CCSS math to this point. I don’t know why that is.
Lane, I don’t know why either, but IM&E is planning to organize more workshops like the upcoming one in New Orleans.
I’m looking forward to the workshop in New Orleans. We really need the content specific math information and plans to move professional development forward. I appreciate the work that IM&E is doing to address these needs. Thank you!
Bill,
I work with teachers in multiplie school districts and have had the same reocurring question. What does “mastery” mean regarding the CCSS for math? Teachers are not sure if “mastery” in each grade level is referred to a certain percent or something else. Any explanation would be greatly appreciated! Thanks for this blog – it has helped answer a lot of questions!!!!
Matisha, I don’t know the answer to this question. Mastery is not a word used in the standards, so you would have to ask the people who are using it.
My question is about the following standard: MCC.7.SP.3 … measuring the difference between the centers by expressing it as a multiple of a measure of variability. The Illustrative Math Project task for this standard states, “The difference in means of 1.5 million is only on the order of 1/3 of the MADs, indicating that the means are not far apart in light of the variation in populations among the states.” Since comparing the difference in means to a variation of the MADs is not something that I’ve ever seen done before (let alone in 7th grade), where would be a good place to go to get a good understanding of why it makes sense to compare these statistics in this manner. In essence, I need to make sense of this myself, before I can make it make sense to my 7th graders. HELP!
Pam, have you already looked at the 6–8 Statistics and Probability Progression? Please let me know if that helps.
Yes, I have. It lays a good foundation for the first part of that standard, but says nothing about measuring the difference between means or medians as a multiple of mean absolute deviation. It’s the second part of the standard that is giving me trouble.
Pam, I don’t like to play statistics educator when my background and experience is in math, so I’ll refer you to the following two things from the American Statistical Association.
Description of ASA education resources: http://www.amstat.org/education/pdfs/EducationResources.pdf.
The Meeting Within a Meeting (MWM) Statistics Workshop for Mathematics and Science Teachers will help middle and high school teachers teach the increased statistics content in the Common Core State Standards. The MWM statistics workshop will be held in conjunction with the Joint Statistical Meetings on Tuesday, July 31 and Wednesday, August 1 at the Hilton San Diego Bayfront with separate middle and high school strands. The registration fee is $50, which includes materials and refreshments. Optional graduate credit and limited lodging reimbursement is also available. More information and registration for the MWM workshop is available at http://www.amstat.org/education/mwm/.
Pam, sorry to reply to myself but I don’t see a spot to reply to you.
I don’t like to play statistics educator when my background and experience is in math, so I’ll refer you to the following two things from the American Statistical Association.
Description of ASA education resources: http://www.amstat.org/education/pdfs/EducationResources.pdf.
The Meeting Within a Meeting (MWM) Statistics Workshop for Mathematics and Science Teachers will help middle and high school teachers teach the increased statistics content in the Common Core State Standards. The MWM statistics workshop will be held in conjunction with the Joint Statistical Meetings on Tuesday, July 31 and Wednesday, August 1 at the Hilton San Diego Bayfront with separate middle and high school strands. The registration fee is $50, which includes materials and refreshments. Optional graduate credit and limited lodging reimbursement is also available. More information and registration for the MWM workshop is available at http://www.amstat.org/education/mwm/.
Should line plots be plotted on a line or a line segment. The example in the progressions is a line segment, but all of the examples I have seen in textbooks are plotted on a line. Which is correct? Or does it depend on the context of the data?
I’m not sure I understand the question. Is this about how the endpoints of the line are indicated? That’s a matter of the convention chosen within a particular curriculum, I think (also a matter of context, as you say).
There is a sample grade one “core aligned” module which asks students to use an inch and cm ruler. Doesn’t the core introduce ruler measures in grade 2?
You are correct that ruler measure is not required in Grade 1. In grade 1 students start to work with the idea of using a standard length unit to measure, as in 1.MD.2:
Express the length of an object as a whole number of length units, by laying multiple copies of a shorter object (the length unit) end to end; understand that the length measurement of an object is the number of same-size length units that span it with no gaps or overlaps.
The document seems to end on page 35 of 38. Is the pagination in error or are pages missing from the end?
Hi Howard,
I think your comment was disconnected from the original source. Can you clarify which document you are referring to?
Thanks!
Ashli
The High School Math Scope and Sequence….the bottom of the last page says 35 of 38.
I’ve asked Patrick Callahan if he can send me a more complete document.
Official word from Patrick Callahan is that it’s a pagination error.
Here is a question involving Geometry at the Kindergarten and first grade levels.
My county is currently developing a Scope & Sequence for both grades. During this process, we were tasked with unwrapping the standards and developing unit plans of study. In comparing some of the geometry standards at K and 1, some questions were brought up, mainly involving K.G.1, K.G.2, K.G.4 and 1.G.1. The first grade team assumed that first graders would begin using defining attributes to determine proper names and classification of shapes, and that kindergarteners would have been recognizing shapes mainly by sight. The kindergarten team felt that kindergarteners would begin identifying, classifying and naming shapes using attributes, mainly number of sides and vertices. The team also felt that many misconceptions would be developed if students were only expected to use visual recognition to identify shapes. We sort of came to an agreement that in K, students might take a single shape and be able to define it based on sides or vertices. “I know this is a triangle because it has 3 sides” Whereas in 1st, students might take the attribute of 3 sides and identify all triangles from a set of shapes.
Without the geometry progression documents, is there a better explanation of the difference between these two grade level geometry standards and expectations?
I think having an expectation that a Kindergartner says “I know this is a triangle because it has 3 sides” goes beyond what is called for in the Kindergarten standards. The relevant cluster is:
K.G. Identify and describe shapes (squares, circles, triangles, rectangles, hexagons, cubes, cones, cylinders, and spheres).
Compare this with
1.G.1. Distinguish between defining attributes (e.g., triangles are closed and three-sided) versus non-defining attributes (e.g., color, orientation, overall size) ; build and draw shapes to possess defining attributes.
It seems to me that the progression is pretty clear here. Of course, as always, that which is not stated is not thereby forbidden; if the definition of a triangle in terms of its attributes comes up naturally in a Kindergarten class, and students seem to be learning from it, then that’s good. But the standards do not require it.
In grade 3 students are to understand the properties of multiplication and the relationship between multiplication and division, 3.OA.5 and 3.OA.6. Regarding Distributive property I’ve seen variations in the interpretations of this in multiple organization and/or state documents – ranging from no appearance of parentheses to beyond what I’m seeing in the standards. 3.OA.7 also includes properties as well. Could you please elaborate on the use of parentheses at this level and clarify these standards.
I think this it a matter of curriculum design exactly when to introduce parentheses. On the one hand, there is no explicit requirement to use parentheses until Grade 5. On the other hand, there’s a footnote on 3.OA.8 that says “This standard is limited to problems posed with whole numbers and having whole-number answers; students should know how to perform operations in the conventional order when there are no parentheses to specify a particular order (Order of Operations).” This suggests that parentheses might well be used much earlier. My own preference would be we start to use them when it becomes difficult to say what you want to say without them, and this would probably be in Grade 3.
Bill,
I had a question today from one of our districts about 3.G.2. In the NF domain we restrict denominators to 2, 3, 4, 6, and 8. Does the same restriction apply to partitioning shapes in 3.G.2 or should students be allowed to make as many partitions as they like?
David, it’s seems a natural interpretation to apply this restriction to 3.G.2, since part of that standards says “Express the area of each part as a unit fraction of the whole.”
Regarding proportional reasoning. I understand major US textbook companies have published “CCSS-alligned” textbooks that do proportions the old-fashioned way instead of determining the constant of variation per CCSS. Has anyone seen a textbook that shows the progressions correctly? Does anyone know of a textbook source from one of the model countries (in any language)? We don’t have to be able to read the text to follow the examples. Lots of folks are questioning whether the progressions are a new US invention or whether they are truly modeled after a high-performing country’s curriculum, so PDers would gain credibility if they had access to an original source. It would be worth the cost, whatever it is, to have an example set of textboooks from, say, Singapore; but again lots of American companies say their textbooks are modeled after Singapore and obviously we can’t just take their word for it.
Lane, I know of three US sources of textbooks from other countries (which I’ve listed below). I’m trying to be brief here, but will try to put something more comprehensive on my blog in the next few days.
I think your question splits into three parts:
1. the term “progression.” The terms “learning progression” and (related but not identical) “learning trajectory” seem to be inventions of US mathematics education researchers.
2. the concept of “progression.” in my opinion, the idea of “learning progression” is implicit in textbooks and other curriculum documents from outside the US. For example, check out the discussion of the central sequence of the knowledge package for subtraction with regrouping in Liping Ma’s book Knowing and Teaching Elementary Mathematics that starts on p. 15 or for the knowledge package on multidigit multiplication that starts on p. 45 (you can see these via Google Books).
3. the content and order of the CCSS progressions as compared with those of other countries. The CCSS states two types of sources in the list of works consulted. These include: documents of other countries (and analyses of those documents), articles on US research on learning trajectories. So, I think the short answer is yes, the CCSS progressions are a US invention, combining US research and progressions from other countries. However, as the work of Schmidt and others points out, progressions in those other countries aren’t all that different from each other (this of course depends on the level of detail).
Many other countries do not have “standards” but have documents which are more or less comparable with names like “course of study” or “syllabus.” Links to those for several countries (including Japan and Hong Kong) are here: http://hrd.apec.org/index.php/Mathematics_Standards_in_APEC_Economies
You don’t need to pay money for textbooks to get evidence about progressions and the CCSS. There are two types of sources: US research on learning trajectories and documents of other countries (and analyses of those documents). Just to be brief (or at least not incredibly long), I’ll only comment on the latter, but note that both types are listed in the “works consulted” in the CCSS.
Many other countries do not have “standards” but have documents which are more or less comparable with names like “course of study” or “syllabus.” Links to those for several countries (including Japan and Hong Kong) are here: http://hrd.apec.org/index.php/Mathematics_Standards_in_APEC_Economies
I’ve discussed comparisons of CCSS and documents from other countries on my blog: http://mathedck.wordpress.com/2011/09/06/strange-accounts-of-the-common-core-state-standards/
Here are the textbook sources that I know. Note that they aren’t necessarily going show things that are identical to what’s in the Progressions (for example, there’s no guarantee that terminology will be identical to the US or even among other countries), but there’s a lot of resemblance).
Singapore Math (www.singaporemath.com) has Singapore textbooks (which were originally written for English-speaking Singapore students) adapted for the US. I think this mainly means that the names of things and British spelling and terms (e.g., “ring it” for “circle it”) are adapted to a US audience. I don’t think they have the teachers manuals for the books. (I do, and I find them useful.)
The University of Chicago School Mathematics Project (http://ucsmp.uchicago.edu/resources/translations/) has translations of Japanese textbooks for grades 7-9 and Russian grades 1-3. (It says that the American Mathematical Society has translations of Japanese textbooks for later grades, but I didn’t see them on the AMS web site and suspect that they may have sold out recently when they were on sale.)
Global Education Resources (GER, http://www.globaledresources.com/) has translations of Japanese textbooks for grades 1-6. It’s also got translations of the teaching guides for grades 1-6 and for grades 7-9, and lots of other things, some of which are free of charge. You can download (free of charge) some translations of the teachers manuals for one textbook series that GER translated from http://lessonresearch.net/nsf_toolkit.html. These are really nice (I worked on editing the translations) as are the textbooks. You can get a sense of what might be called a “progressions way of thinking” in Learning Across Boundaries: U.S.–Japan Collaboration in Mathematics, Science and Technology Education (free and downloadable at http://www.lessonresearch.net/LOB1.pdf). For example, check out the piece that begins on p. 261. In discussing “research lessons” (special lessons created by groups of Japanese teachers as a result of “lesson study”), a Japanese professor of mathematics education says:
A research lesson is only one lesson. However, in doing research lessons we are not thinking
about only one lesson. We need to think about the entire unit and how it’s related to other
grade levels. That is very important.
He continues (pp. 262-266) by illustrating how that might be done for a lesson on estimating the area of a circle, using excerpts from the GER translations of Japanese textbooks.
Sorry not to put live links, but it is time consuming and I seem not be doing well with this recently (maybe the blog interface has changed).
Fantastic. This will give me some additional summer reading!
A question arose today regarding when to introduce division problems with remainders. Thoughts?
This happens in Grade 4:
4.OA.3 Solve multistep word problems posed with whole numbers and having whole-number answers using the four operations, including problems in which remainders must be interpreted. Represent these problems using equations with a letter standing for the unknown quantity. Assess the reasonableness of answers using mental computation and estimation strategies including rounding.
and
4.NBT.6 Find whole-number quotients and remainders with up to four-digit dividends and one-digit divisors, using strategies based on place value, the properties of operations, and/or the relationship between multiplication and division. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models.
The The High School Math Scope and Sequence that I’ve seen using your website has Exponential Functions and Rational and Polynomial Functions in Algebra 2, but New York State has them in Algebra 1. The Common Core isn’t so common, anymore!
The high school standards are not arranged into courses. States wanted this flexibility, so that some could pursue a traditional sequence and some could pursue an integrated sequence. That said, I think you’ll begin to find more uniformity once the assessment consortia come out with high school course boundaries.
I am very interested in the answer to Patrick’s question:
———————————————————–
Patrick says:
April 19, 2012 at 9:16 am
One of ther question that I would have is… has anyone taken a poll of the CC states to see which states have adopted the Traditional Model at the HS level vs. the Integrated approach? This could be useful as we begin to share information/resources, etc. Thank you.
————————————————————-
I’m a teacher at a boarding school in Utah, and many of our students come from California. Utah is going with the integrated model for its high school math. In California, at what level is the “integrated vs traditional model” decision made? I mean, will I have students next year from California who were taking “Integrated Math 9” and others of the same grade taking traditional “Algebra One?”
I think the integrated model is less-adopted across the nation. I surmise this because of how many Utah entities (the State, a few districts, and a few schools) are currently actually writing their own online textbooks just for “Secondary Math I (i.e., Integrated Math 9).”
Hi Dr. McCallum
We hit a snag with this standard:
A-SSE.1 – Interpret expressions that represent a quantity in terms of its context.
Interpret parts of an expression, such as terms, factors, and coefficients.
Interpret complicated expressions by viewing one or more of their parts as a single entity. For example, interpret P(1+r)n as the product of P and a factor not depending on P.
Our question is….What does the word “interpret parts of an expression such as factors” here mean? How does one interpret a factor? Does this standard merely mean that we identify parts of an expression? If that is the case, why is the wording used “interpret” instead of “describe” or “identify?”
Thank you 🙂
Note that the standard calls for you to make the interpretation in terms of a context. That’s important. Given a naked expression like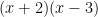 there’s not much that you can say about the factors except that they are factors. But an expression like
there’s not much that you can say about the factors except that they are factors. But an expression like 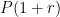 might arise in a context where an amount of money
might arise in a context where an amount of money 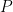 is increased by an interest rate
is increased by an interest rate  . Then the interpretation would go beyond just recognizing
. Then the interpretation would go beyond just recognizing  and
and  as factors, to include relating each factor to the context and to the way interest is computed.
as factors, to include relating each factor to the context and to the way interest is computed.
PARCC’s “major clusters” are not the same as the critical areas of the Common Core.
I’m confused! Can you help explain?!
Sarah Renninger
Math Coach
New Jersey
The critical areas are an introduction to the standards at each grade level, cast into more friendly language, but they are still just a flat survey, and do not capture the carefully designed structure of the standards themselves and their progression across grade levels. The cluster headings are signposts for that structure. Often they communicate the point of a group of specific standards, rather in the way that a topic sentence communicates the point of the remaining sentences in the paragraph. So, if you want assessments to capture the structure of the standards, and avoid being a flat checklist, it makes sense to organize them around the clusters rather than around the critical areas.
Thanks for this wonderful help, Bill.
Regarding K.CC.1 “Count to 100 by ones and by tens,” I am wondering if the idea is for the student to be able to speak the two sequences rather than actually count objects. Sometimes, students live through 90 hours of calendar time per year for a number of years and then when asked to count a collection by fives, point to each object and speak a multiple of five. They don’t use the sequence to actually organize the objects in the collection and find out how many there are. So instead of 20 objects, they will respond with 100 objects.
It doesn’t seem right to expect a kindergarten student to manipulate 100 objects into groups of 10 to count them by tens. Can you give some guidance?
I think as I study a bit more I can answer my own question. Standards 1, 2, and 3 really are about the sequence and standards 4 and 5 are about how many and guidance about the range of number is given.
Lynn, yes, you are absolutely right, and you have answered your own question correctly! K.CC.1 is about the sequence. The language of the cluster headings is part of the standards, in addition to the standards themselves.
Bill,
In 5.NF.1, the general formula for fraction addition is given as:
a/b + c/d = (ad+bc)/bd
I would write it as:
(ad+bc)/(bd)
I agree that we all know the order of operations that the author intended, but is it clear from what is written, and a good example of how to write fractions?
Really, it should be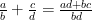 , but the typesetting was limited. I can see your point that there should be been extra parentheses around the
, but the typesetting was limited. I can see your point that there should be been extra parentheses around the  when the fraction was shilled.
when the fraction was shilled.
My concern is when do they begin to understand LCD because that memorized formula is a huge stumbling block to Algebra 2 students working with rational expressions.
Lane, I don’t think I understand the question, can you give an example?
In the formula under discussion, bd is the “easy way” to find a common denominator. However, students who are not fluent in converting to a least common denominator LCD are typically overwhelmed when tasked with solving rational equations. In general, if we have x/ab + y/bc = z/ac where a,b,c, are prime polynomials, the LCD is abc, not (abbcad). For instance, if a student needs to solve (3y)/(y^2+5y+6) + 2/(y^2 +y-2) = (2y-1)/(y^2+2y-3) and multiplies all 3 denominators together, then proceeds to multiply the numerators by all the denominators, they end up with high-degree polynomials in the numerator. Yet if the students have been getting away with bd for years (because their lower level teachers don’t know what’s ahead) and we try to get them to find LCD, a small war ensues and we are accused of making things more difficult than they need to be.
Lane,
I’m glad someone else is fighting the good fight. Let’s compare strategies for remediation.
Brad, bburkman@lsmsa.edu.
Ha! Sounds like Dr. McCallum will need to start another page for that. I have taught thru Calculus, but prefer analyzing how right-brainers can be taught to “see” what mathees see (hurray Smartboard). A big help is learning to fluently decompose. Working with high schoolers who have memorized and confused a bunch of rules and steps, I insist they break everything down to primes until they begin to discover the rules on their own: LCD, GCF, working with exponents, factoring out perfect squares from radicals, rationalizing…always with primes until they see. But connections are best built over time, not as a last-ditch effort to save them. I believe CCSS is at least ‘saying’ comprehension is better than memorized formulas. Whether it pans out that way I believe depends largely on this web site.
“5.NF.1, the general formula for fraction addition is given as: a/b + c/d = (ad+bc)/bd”
is another formula to mess up; why not use multiplicative identity on primes til they see?
I don’t teach HS, but I think a natural formula elementary children will derive is a/b + c/d = (ad + bc)/(bd). In the way fractions are laid out in the CCSS, the line of reasoning goes something like this:
In Grades 3 & 4, students learned that a/b is a pieces of 1/b units. So, they find it relatively easy to calculate 3/5 + 4/5 because 3 1/5 units and 4 1/5 units together will be 3+4 1/5 units, or 7/5. Then, in Grade 5, when they encounter 2/3 + 3/4, they would say, we can’t because 2 and 3 refer to different units. But, they learned in Grades 3 and 4, some fractions may look different but stand for the same numbers – and in Grade 4 they learned how to create equivalent fractions. So, they could say, well, 2/3 doesn’t always have to look that way (and 3/4 can look different, too). So, they find a common unit that can be used to express both 2/3 and 3/4. They realize 1/12 is an easy option since the way to create equivalent fractions is to multiply both the numerator and the denominator by the same number. So, if you have two unlike denominators, then one easy common unit is to use the product of the denominator as the common units.
I tend to think when students see the need, that’s the best time to teach a relevant mathematical idea. If calculation involving rational expressions is where the usefulness of LCD comes in, then maybe that’s when the idea should be discussed.
Your argument is well taken. I would help them see the need for LCD as they need to work with larger denominators. The frustration level we experience with the kids in high school doesn’t need to be. I would push for exploration of LCD a year after bd, beginning with adding fourths to halves with the LCD of 4ths instead of 8ths. Shortly after that time, I believe they should be working with prime factorizations to find the LCD in order to avoid a lot of reducing in the end. If they understand prime factorization, that tool bypasses a lot of mindless “steps” to confuse from Pre-Algebra through Algebra 2.
I apologize for multiple posts, but I was also wondering about the example Lane gave. After student multiply both sides of the equation with the product of 3 denominators, why do they multiply the terms out to get a higher order equations? Why not factor those expressions that were the denominators? Then, you have some factors that are common in all 3 terms, allowing us to cancel (divide) them out? Then, you will have a quadratic equation at the end. Wouldn’t the whole process about equally complicated as finding the LCD?
In order to cancel a factor from the numerator, of course, it has to be a common factor with the denominator, in essence “1.” In solving rational equations, we sometimes get very messy numerators where we have to 1) combine like terms, 2) factor, 3) cancel. If we have created higher power terms by not getting the LEAST common denominator, the students do not have the tools to easily factor them. They would have factor by finding zeros in their grapher and dividing them out or apply the rational root theorem…very frustrating to throw all that into one problem. If they can find the LCD, then it is very doable.
I agree with Tad that, “when students see the need, that’s the best time to teach a relevant mathematical idea.” And, the way he talks about introducing the addition of fractions with unlike denominators sounds right to me (with the use of visual fraction models to support understanding of the what’s happening when we multiply both the numerator and the denominator of one fraction each by the same number). But every 4th grade standard related to the addition or subtraction of fractions explicitly states “with like denominators.” Another cluster does require students to find common denominators, but the only application of this that is stated in the 4th grade standards is to compare fractions. The cluster on operations with fractions very clearly states “with like denominators” and, therefore, seems to exclude uncommon denominators.
5.NF.1 (“Add and subtract fractions with unlike denominators…”) is the first standard that explicitly addresses the addition and subtraction of fractions with unlike denominators.
Based on this, it seems to me that the quote from page 10 the Progression for NF that Eric raised (“In Grade 4, students calculate sums of fractions with different denominators…”) would refer to a natural extension of 4th grade standards, but is neither required nor forbidden by the standards themselves.
If this is not the correct interpretation, please advise soon, as I know a LOT of districts that will need to seriously alter plans!
Thanks,
Brian
I, too, was surprised when I read the statement mentioned by Eric in the draft progression document. I think it is clear that 2/3 + 3/4 is in Grade 5, but 2/3 + 5/6 will be in Grade 4 according to the progression document but in Grade 5 if we just read the CCSS. I supposed the progression documents are supposed to be an elaboration, maybe the authors of the CCSS meant to include 2/3 + 5/6 in Grade 4.
If you compare 2/3 + 3/4 and 2/3 + 5/6, perhaps 2/3 + 5/6 is easier procedurally (to find the common unit) but they are equal conceptually (let’s make the unit the same). So, comparing fractions with unlike denominator after learning how to create equivalent fractions (and learning how to add fractions like 2/3 + 5/6) but not add/subtract fractions with unlike denominators (where neither is a multiple of the other) is like having to stop an interesting story right before the end and told to wait till next year to finish it — to me.
lol. Thanks, Tad. Your interpretation is consistent with mine… and your analogy is great!
Brian & Tad,
I agree with you both, that “when students see the need, that’s the best time to teach a relevant mathematical idea.” If I read Lane correctly, the concern of high school teachers (including myself) is that fraction addition in CCSS-M seems to stop in fifth grade. In sixth grade students learn to find the lcm, but they don’t apply it to fractions to find the lcd. Then in high school, Tad throws them a sum of rational expressions whose elementary-school equivalent is 1/6 + 1/8 + 1/9. Our students want to use 6*8*9 = 432 as the common denominator, when they could use 72. Between fifth and tenth grade, students do not expand their understanding of fraction addition. If in sixth or seventh grade we had them use their new skills in finding least common multiples to subtract
7/30 – 5/42 = 7(5*6) – 5/(7*6) = (49 – 25)/(5*6*7) = 24/(5*6*7) = 4/35
then they’d be ready for Lane’s question in algebra.
Exactly! I’m so glad you succinctly summed it up here. We should be building a continuum, stimulating the “need to know” for the next idea, instead of setting the kids up for a big leap of frustration. Very few kids understand LCD in the abstract sense (rational eqns) if they haven’t already grasped LCD numerically. This is one way we lose a lot of Algebra 2 students. Decomposition is a basic building block for number sense so I don’t understand why CCSS would leave this gap. I think the only way it would make sense if we decided not to teach rational functions.
I’ve been thinking about how to respond to all this. I was just chatting with my colleague Cody Patterson and he said it in a way that I found very useful: finding least common denominators is a strategy, not an essential component of fraction addition (either numerical or algebraic). It’s important to separate out the task of understanding fraction addition as an operation from the task of finding efficient strategies one might use to find answers in special cases. We don’t want students to think the strategies are the same thing as the operations themselves. Job one is understanding the operation.Tad summarizes that understanding well: in adding fractions you express each fraction in terms of a common unit. The natural common unit is the unit fraction whose denominator is the product of the denominators of the addends. And this is only common unit that exists in general, so it’s the only one that leads to a general formula. All this is difficult enough conceptually; it muddies the waters to worry about special cases where you might be able to find a smaller common unit. Worse, it might make kids think that somehow finding least common denominators is an essential part of fraction addition (I’ve certainly met students who seem to think that). And, since there is no formula for “adding fractions by finding a least common denominator”, insisting on it gets in the way arriving at a general formula; the general formula becomes something extra to memorize later, rather than an essential understanding of fraction addition as a general operation. Fraction addition becomes an arcane art. The calculation
is 100% mathematically correct. There is not anything even a little bit wrong with it. Once kids have a solid understanding of fraction addition, and if there is time in the curriculum, it is worthwhile pointing out that the answer is equivalent to and exploring what strategies you might have used to get that answer.
and exploring what strategies you might have used to get that answer.
The same comments applies to Lane’s original example. One strategy for solving this problem is to multiply both sides by the least common denominator. But as Tad pointed out, another reasonable strategy is to multiply both sides by the product of all the denominators and then cancel common factors from both sides of the equation before expanding. This takes slightly more ink, but provides an opportunity to discuss an important strategy in algebraic manipulation, namely the advantage sometimes of keeping expressions in factored form rather than blindly expanding them out. There are advantages to both strategies, but neither is sacred.
I get it! . The #1 topic that causes our Algebra 2 students to become overwhelmed and fail is over things like this and I really apprciate your taking the time to explain it in a way that makes sense to me. Thanks for taking the time
Bill et at,
I’m going to disagree, on several points.
First, there IS a general formula for adding fractions using the least common denominator. In a/b + c/d, let g=gcd(b,d). Then there are relatively prime integers (or polynomials) e and f such that b=eg and d=fg.
a/b + c/d = a/(eg) + c/(fg) = (af+ce)/(efg).
The formula works for ratios of both integers and polynomials, and covers the case when g=1.
There is no “the” general formula; there are two. The one in the Standards is the general brute-force formula, like killing a fly with a bazooka. The formula I’ve given is the general elegant formula, which uses the basic number theory the Standards say students should learn in sixth grade.
I’m also going to disagree with Bill about the product of the denominators being the “natural common unit…the only common unit that exists in general.” The “efg” above exists in general, because g can be 1. The “bd” does require less forethought, but I don’t know why that’s more “natural.”
Let’s look at the three methods mentioned for solving Lane’s sum of ratios of polynomials.
Here’s the result of multiplying both sides by the product of the denominators and expanding.
y^5 – 7y^3 + 22y^2 + 32y – 48 = 0
which is a nice exercise in the Rational Roots Theorem, especially since the sum of the roots is zero.
When we apply Tad’s strategy, here’s what we get.
3y(y^2 + y – 2)(y^2 + 2y – 3) + 2(y^2 + 5y + 6)(y^2 + 2y – 3) = (2y-1)(y^2 + 5y + 6)(y^2 + y – 2)
3y(y+2)(y-1)(y+3)(y-1) + 2(y+2)(y+3)(y+3)(y-1) = (2y-1)(y+2)(y+3)(y+2)(y-1)
Now divide both sides by (y+2)(y+3)(y-1).
3y(y-1) + 2(y+3) = (2y-1)(y+2)
y^2 – 4y + 8 = 0
Easier at the end, and a great occasion to talk about canceling only one of a the (y+2)’s, one of the (y+3)’s, and one of the (y-1)’s.
If we’d used the least common denominator, we would have skipped straight to 3y(y-1) + 2(y+3) = (2y-1)(y+2).
I understand wanting students to see the big picture and not get lost in the details, but here is where high-school students get lost in the details because their elementary-school teachers were trying to keep them from getting lost in the details.
I would like the Standards to say that, every year, teachers need to review, remediate, practice, connect, and deepen students’ understanding of topics from previous years. Then, in high school, students will be ready to move from ratios of integers to ratios of polynomials.
The fairly consistent pattern I see is a student arrives at high school weak with fractions, makes it to Algebra 2 and then fails half way through because so much depends on fractions there. So what Dr. McC is saying about consistently using bd all the way through will undoubtedly bring along more students. The faster students can be easily nudged into experimenting with efficient means such as LCD without overwhelming the slower students. I also agree with you, Brad, when you say fractions need consistent remediation, reinforcement and exploration all along the way for purposes of retention and enrichment, or large percentages of students will simply avoid fractions whenever they surface and, in the end, fail Algebra 2. I would place fraction remediation up there with speech/language issues.
Although I agree that students in MS and HS will be given opportunities to work with fractions regularly, I hope it will not take the form of a “review unit” that we often see in commonly available textbooks. I think it is not just students who “avoid fractions.” I must confess I am guilty of often not including fractions as we investigate other math topics. Even in the CCSS, so many of the examples involve only whole numbers – for example, 7.EE.4a says, “for example, the perimeter of a rectangle is 54 cm. Its length is 6 cm. What is its width?” even though the standard itself says “Solve word problems leading to equations of the form px + q = r and p(x + q) = r, where p, q, and r are specific RATIONAL numbers.” I know we do it to make sure that students’ difficulty with fractions will not hinder their learning of other math concepts, but I think I need to incorporate fractions (and decimal numbers) more – perhaps not at the introductory stage of a new concept, but definitely as students try to solidify their understanding of the new idea.
It seems my question might have gotten stuck in the moderation queue, so I’m reposting here and would love some advice 🙂
Hi! Thanks for providing the opportunity to ask questions about the Common Core Standards. I just wanted to clarify a few things in the high school standards:
(1) G-GPE.4 Students are asked to “Use coordinates to prove simple geometric theorems algebraically” and the given examples are about proving that four points form a rectangle or that a point lies on a circle. Are there other types of “simple geometric theorems” that students should be familiar with, or guidance I can use to interpret the word “simple”?
(2) G-GC.2 Similarly, students are asked to “identify and describe relationships…” in circles. Should this include secant theorems, or just the more obvious angle theorems and tangent theorems?
(3) G-GMD.1 reads “Identify the shapes of two-dimensional cross-sections of three-dimensional
objects.” Since 7.G.3 reads “Describe the two-dimensional figures that result from slicing three-dimensional figures” and specifies right rectangular prisms and right rectangular pyramids, is it safe to assume that the high school standard includes cross-sections of any and all 3D objects beyond right rectangular prisms and right rectangular pyramids?
(4) I’m not seeing solving absolute value equations (e.g. |x – 3| = 5) in the standards, although I do see absolute value of real numbers in middle school and then graphs of absolute value functions in high school. Is it implied but not explicitly required that students should be able to solve absolute value equations?
(5) A-APR.3 and F-IF.7 use the language of “when suitable factorizations are available” to describe when students should be finding roots of polynomial and rational functions. Does this mean that students should be comfortable finding factors using GCF, grouping, sums/differences of squares, but not long division? Or not long division with remainders? Where do we draw the line with what is “suitable”?
(6) I see references to the properties of operations (commutative, associative, etc.) in lower elementary standards about addition and multiplication, and in high school standards relating to complex numbers and matrices, but not as they relate to algebraic expressions. Can I interpret this to mean that while students should be familiar with and able to flexibly use the properties, they will not be assessed on being able to name specific properties?
Thank you so much for your time and help!
(1) The essential point of G-GPE.4 is to use coordinates to prove theorems; how far one goes with this depends on the curriculum as a whole, not only on this standard. That is, different curricula might spend different amounts of time on different standards. The Illustrative Mathematics project will eventually supply some examples.
(2) Same answer here; the standard certainly does not insist on the secant theorems, and a curriculum could satisfy the standards without them. But these are beautiful theorems, worth including if there is time.
(3) I think you meant G-GMD.4. Certainly, any shape is fair came, but your formulation makes me a bit nervous … we don’t want to get carried away with this. Again, the idea is to get kids thinking about shapes of cross sections. The idea is not to have some long exhaustive list of shapes and expect them to be able to deal with every single one on an assessment.
I’ll answer the next three questions in a later post.
4.NF.3 says, “Understand a fraction a/b with a > 1 as a sum of fractions 1/b.” This seems to be implying addition of fractions with LIKE denominators. Then reading parts a,b,c,and d, it mentions LIKE denominators, but never UNLIKE denominators. However, when reading the Progression document for NF, it says on pg. 10 under the Grade 5 heading, “In Grade 4, students calculate sums of fractions with different denominators where one denominator is a divisor of the other, so that only one fraction has to be changed.” Then it gives an example of 1/3 + 1/6. In all of the Grade 4 Progression, in the section titled “Adding and subtracting fractions,” it never mentions this idea of adding unlike denominators when one is the divisor of the other. In fact, ALL of the examples show sums and differences with LIKE denominators. Should we be giving 4th grade students problems and questions relating to sums of fractions with UNLIKE denominators. I can see where 4.NF.3a could lend itself to this type of thinking, but with the root standard defining it as “sums of fractions 1/b,” this seems to be contradictory.
I think the Progression is misleading here. In general students are adding fractions with like denominators in Grade 4. There is one place where they add fractions with unlike denominators:
The footnote says:
So the 1/3 + 1/6 example is consistent with the standard and the footnote, but is not required.
Hello! I just went through my first year of trying to implement the Common Core Math Standards for 8th grade and I do not feel like I did a great job. I just watched Phil Daro’s video about how we teach to get answers instead of the math. I want to be that teacher that lets the students explore the math instead of me telling them how to get there. Do you know where I can find learning tasks, messy problems, thinking problems, what ever you want to call them, for 8th grade common core so the students in my class don’t worry about answers and worry about the process? I know PARCC will be putting out sample tasks this summer, but I would love to start working on things NOW! 🙂 I don’t feel like I can “create” problems myself that are not a traditional type of story problem.
Thank you for your time,
Julie Brandolino
Julie, Illustrative Mathematics will eventually have a collection of tasks of all sorts, and it will also be a place where you can interact with others and learn to create such tasks. I know we are not there yet, but it’s worth keeping in mind.
Also, I wouldn’t say that Phil was talking against traditional story problems, or in favor of messy problems, or indeed expressing a preference for any particular type of problem. Rather, he was suggesting that we focus on how a problem is used, whatever type it is. Story problems can be great learning problems, if students are not encouraged to solve them by key word search. And “messy” problems can be very formulaic.
Just attended the conference in New Orleans. Very valuable. If you have the opportunity to attend one in the future, it is with your time!
Someone sent me this question:
Here is an answer I gave to a similar question about patterning and skip counting elsewhere on this blog (in response to this thread.
I ran across a standard in the common core that has bothered me and has me thinking and I was wondering if you could clarify it for me. The standard is G.CO.9 “Prove theorems about lines and angles.” It then goes on to give some examples of the theorems that students will prove. When it comes to the parallel lines cut by a transversal examples, it uses alternate interior angles are congruent and corresponding angles are congruent. The problem I am having is the one about corresponding angles. In every book I have used, corresponding angles congruent is a postulate and not a theorem and I thought that postulates were the foundations we accepted and then built the theorems from it. Can you please help me understand this?
The key here is to note the previous cluster heading, “Understand congruence in terms of transformations.” You can prove that corresponding angles are congruent by, for example, performing a translation along the direction of the transversal. You still have to assume something, of course, namely the fact that the translation of an angle is a congruent angle; the fundamental properties of transformations are taken as the postulates. (See 8.G.1 for the foundations of this.) And you have to have already established that a translation of a line is a parallel line.
Dear Mr. McCallum,
To whom might I address this typo (http://i.imgur.com/jJKtM.gif) I found in Appendix A?
Thanks,
Tom James
This looks as if it comes from p. 20 of the model course pathways document from Achieve. I suggest you send a message about the typo via their contact form: http://www.achieve.org/contact
Thanks, Cathy. I’ve used the form to send Achieve a message.
We have been studying + standard N-CN 5. The question we have is about the interpretation of the multiplication of complex numbers geometrically. Does this mean scalar multipiication or the multiplication of two complex numbers? We are able to do the multiplication of complex numbers algebraically, but are finding very little anywhere about how to do it geometrically. The example of the complex numbers cubed also confuses us. We were able to do it using DeMoivre’s Theorem, but not geometrically.
Any clarification or example(s) would be aprreciated.
Dennis, de Moivre’s theorem is part of what is meant here. It is geometric in the sense that it viewed a saying something about the angle in the complex plane between the positive real axis and the ray from the origin to the complex number. Namely, it says that these angles add when you multiply the numbers. The other piece is that the scaling of the magnitude; that is, the magnitude of the product is the product of the magnitudes.
What was the thinking behind leaving Pre-Algebra out of the traditional frameworks in Appendix A? Is it that these subjects are contained in 7th Grade Advanced, or are they in Middle School Algebra I? Or, are you re-thinking the nature of Pre-Algebra as a course itself. Please clarify. The context: I need to make a Year At A Glance for Pre-Algebra since we still teach this course, however, I will use one of the existing grades like 7th Advanced, 8th, or Middle School Algebra I form Appendix A if these are usurping what used to be Pre-Algebra. Forgive me if someone asked this already but there are over a hundred comments. Thanks, Jonathan Haack.
Grades 6-8 were designed as a ramp up to high school algebra; they constitute a designed preparation for algebra (also geometry and statistics and probability), and so the make the notion of Pre-Algebra obsolete. But if you have to give an answer, I guess the closest thing to what you want would be the Accelerated 7th Grade in Appendix A, or maybe you could say that Pre-Algebra is just embedded in Grades 6–8 (or in accelerated Grades 6–7). Although I haven’t looked carefully enough to be sure about this.
Thanks for your response. That was my suspicion, namely, that it was being phased-out, usurped, replaced, etc. So …
Here is what I did: I went through and combined some of the more advanced 7th grade domains, cluster headings, and content standards with those of 8th. I left behind about 6 cluster headings that seemed more basic and 6th grade-based. I inserted those into the 8th grade year-at-a-glance and then grouped them according to Major, Supporting, and Additional topics, under the following assumptions: 1) Students will be assigned a one-year Pre-Algebra class so it needs to contain curriculum that can be covered in one year. 2) Pre-Algebra may eventually be phased-out, re-named, or usurped, however, until then it seems that the “basic” framework for 7th grade and that of 8th most closely resembles what is traditionally taught in such classes.
Here is what resulted:
Unit 1: Real Numbers
– Analyze proportional relationships and use them to solve real-world and mathematical problems. (Reinforcement from 7th grade)
– Know that there are numbers that are not rational, and approximate them by rational numbers. (Reinforcement from 8th grade)
– Apply and extend previous understandings of operations with fractions to add, subtract, multiply, and divide rational numbers. (Reinforcement from 7th grade)
– Solve real-life and mathematical problems using numerical and algebraic expressions and equations. (Reinforcement from 7th grade)
– Work with radicals and integer exponents. (Reinforcement from 8th grade)
Unit 2: Pythagorean Theorem
– Solve real-life and mathematical problems involving angle measure, area, surface area, and volume. (Reinforcement from 7th grade)
– Understand and apply the Pythagorean Theorem. (Reinforcement from 8th grade)
Unit 3: Congruence and Similarity
– Understand congruence and similarity using physical models, transparencies, or geometry software. (Reinforcement from 8th grade)
Unit 4: Linear Relationships
– Understand the connections between proportional relationships, lines, and linear equations. (Reinforcement from 8th grade)
– Analyze and solve linear equations and pairs of simultaneous linear equations. (Reinforcement from 8th grade)
– Define, evaluate, and compare functions. (Reinforcement from 8th grade)
– Use functions to model relationships between quantities. (Reinforcement from 8th grade)
Unit 5: Systems of Linear Relationships
– Define, evaluate, and compare functions. (Reinforcement from 8th grade)
– Use functions to model relationships between quantities. (Reinforcement from 8th grade)
Unit 6: Volume
– Solve real-world and mathematical problems involving volume of cylinders, cones, and spheres.
Unit 7: Patterns in Data
– Investigate chance processes and develop, use, and evaluate probability models. (7th grade required)
Now, there could be an argument made for dropping some 8th grade cluster headings, and adding some 6th grade cluster headings, or vice versa, however, we chose to keep it this large and then on the Year-At-A-Glance file we developed to group the ideas according to importance as stated above, ie., Major, Supporting, Additional. Mr. McCallum, what do you think?
Thanks,
Jonathan Haack
Thanks for taking time to answer all these queries Bill, it’s been immensely useful. I have a question about how to interpret standards that have a sub-standard listed as well. An example is K.CC.4. The statement has this sentence, “Understand the relationship between numbers and quantities; connect counting to cardinality.” What follows next are three more statements labeled a, b, and c. Is the statement I quoted meant to be assessed *in addition to* a, b, and c? Or does the statement merely *summarize* a, b, and c?
On a related note, where would subitizing lie in K? The progressions mention the role of subitizing but there does not seem to be a standard that either perceptual or conceptual subitizing clearly relates to.
Both good questions. There is no one fixed scheme for interpreting the lettered statements in a standard, it really depends on the context. I can think of examples where both your interpretations are correct.
A-SSE.3 is an example of your first interpretation. In that case, the stem “Choose and produce an equivalent form of an expression to reveal and explain properties of the quantity represented by the expression” can apply to any expression students might encounter; the lettered statements make specific ties to quadratic and exponential expressions, but do not limit the standard to those.
8.G.1 is an example of your second interpretation. The stem says ” Verify experimentally the properties of rotations, reflections, and translations”, and then the lettered statements list the properties.
K.CC.4, the example you have given, fits somewhere between the two. I would not say that the stem of the standard is additional to the lettered statements, but neither would I say it summarizes them. Rather, it is a higher level statement that cannot be reduced to them; it holds them together in a certain way. An activity designed to assess this standard might operate at that higher level; see, for example, http://illustrativemathematics.org/illustrations/447, which operates at the level of the cluster heading. The lettered statements give the teacher things to look for during the course of this activity.
These varying interpretations of the lettered statements pose a challenge to assessment, of course, but it is the challenge inherent in trying to preserve in the standards themselves some of the complexity of the knowledge structures they describe.
On subitizing: it’s hard to imagine what a standard would look like. Subitizing is something that kids do naturally, as the progression describes, but I don’t think it’s a required performance at any particular stage, although presumably kids who can’t do it will eventually run into trouble with one or another of the performances that are required.
I’m planning for the upcoming school year and I notice there’s no mention of fraction-decimal-percent conversions in the upper elementary and middle grades standards…any suggestions as to when this should be introduced and studied in depth? My state taught this thoroughly in 5th grade before the onset of CCSS.
Amber, I don’t think that a standard exists that specifically focuses on fraction/decimal/percent as we have traditionally seen this in the past. Instead this is replaced with a deep understanding of how decimals relate to fractions in standard 4.NF.6 and then coming back in standard 6.RP.3c with a deep understanding of percent as a rate per 100 (30% of a quantity is 30/100 times the quantity).
The students will end up with a deep understanding of what decimals are and what percent means and will then be able to see relationships between the three forms of number.
As stated, they have introductory knowledge in prior grades converting fractions and decimals (10ths and 100ths), and then percents as fractions in Grade 6. But I think what you are looking for is in Grade 7. Standard 7.NS.2d covers fractions to decimals, formalizing the language of terminating/repeating. Standard 7.EE.3 seems to bring everything together, requiring “converting between forms as appropriate.”
Thanks very much Leandra and Monique! Let me add that the standards avoid talking about “conversion” between fractions, decimals, and percents, because it reinforces the misconception that these are all somehow different kinds of numbers, rather than different ways of writing the same number. So, for example, the Grade 4 standard that Leandra pointed out “Use decimal notation for fractions with denominator 10 and 100” certainly includes “converting” 0.25 to 25/100, but says it a different way, namely that 0.25 and 25/100 are different names for the same number. The same comments apply to percents in Grade 6, where 30% is understood to be simply a different way of writing 30/100, rather than a different sort of number called a percent. This is all part of the shift in middle school towards seeing numbers as part of a number system.
Dr. McCallum, I have a few questions concerning 8th grade Transformations, Congruence, and Similarity Standards.
1) Will students need to rotate around a point other than the origin?
2) Will students need to reflect across any line other than the x-axis, y-axis, y=x, and y=-x?
3) Will students need to dilate using a center point other than (0,0)?
We are in the process of writing units and wanted to make sure we were covering the rigor required by the standards.
Thank you for assistance.
Elizabeth
First a general comment on the Grade 8 geometry standards: it is not necessary that all the work on transformations in Grade 8 take place in a plane with coordinates. Students could get hands on experience with transformations using geometry software or a pair of transparences, in which they perform and analyze transformations in a blank plane without coordinates. I think this would be preferable for much of the work.
However, there is one standard that refers to coordinates, and I assume this is the one you are talking about:
Here I think it is reasonable to suppose that the problem is limited to ones students can do with the algebraic tools at their disposal. That would include your (2) and (3), but it wouldn’t even include all rotations about the origin, since you need trigonometry for that. It could include rotations through 90 degrees, and I can imagine a few more transformations that could be used in instruction as challenge problems of an exploratory nature. For example, you could have students figure out that a dilation from a center other than the origin can be achieved by first translating the center to the origin, dilating there, and then translating back again. But I would hate to see this turned into some formulas to be memorized on a test.
Dr. McCallum, we are currently creating our curriculum maps and are confused when we compare fraction common core standards for adding fractions in fourth grade to the progressions in 4th/5th grade on this subject. The common core standards in fourth grade state: use numbers with common denominators; yet, when we read the beginning of the fifth grade progression on this topic, it indicates that “In Grade 4, students calculate sums of fractions with different denominators where one denominator is a divisor of the other.” Is this only with the abstract study of the numbers – composing and decomposing? We’re confused.
This is an error in the progression document: see the discussion here: http://commoncoretools.me/2011/08/12/drafty-draft-of-fractions-progression/#comment-1570
I have a question about G-CO.7. It seems like what the standard asks is something like this: Start with this axiom: “Two plane figures are congruent if and only if one can be mapped to the other by a series of rigid motions.” And maybe a definition: “A rigid motion is a transformation that preserves distance and angle measure.” And possibly another axiom: “If two plane figures have corresponding sides and angles congruent, there exists a (rigid) transformation from one to the other.” And from those starting points, you can deduce that triangles are congruent if and only if corresponding sides and angles are congruent. Is that the essential idea of this standard, or am I missing something?
And then is the thinking behind G-SRT.3 along the same lines?
Thanks very much for any help or thoughts on this!
This is on the right track. Yes, congruence is defined in terms of rigid motions as you describe. However, for the definition of rigid motion, see the glossary, page 87:
So it is taken as an axiom that translations, reflections, and rotations preserve distance and angle, although students are asked in Grade 8 to verify this experimentally (8.G.1).
With these definitions and assumptions, it is possible to prove that two triangles have congruent corresponding sides and angles then there is a rigid motion taking one to the other. First you translate one of the triangles so a pair of corresponding vertices coincides, then you you rotate so that a pair of corresponding sides from that vertex coincides, and possibly reflect so that the other pair of sides lies on the same side of the first one. From this point on, using that angles and distances have been preserved, you can reason that the triangles coincide.
Yes, I know, we should have the geometry progression out where all this is explained with diagrams. Sigh.
This is a big help. Thanks!
Continuing on the subject of geometry…
G.CO.2 discusses using functional notation to describe transformations and G.CO.6 discusses using geometric descriptions of rigid motions to transform figures and predict effects of a rigid motion on a given figure. Specifically what is the difference between the two different modes of description? Is it as simple as using the terms “reflect”, “rotate”, “translate”, or “dialate”?
G.CO.2 does not require the use of function notation, but rather asks that students think of transformation as functions. It is not about notation, and certainly not about creating some horrible catalog of notations for different transformations, but rather about experimenting with transformations. Indeed the cluster heading for these standard is “Experiment with transformations in the plane.” (It’s always a good idea to look at the cluster heading to get a sense of the standard.)
G.CO.6 is more precise, and asks students to work with the precise definition of different transformations. Here one might or might not introduce some notation for different types of transformations; that’s really a curricular decision. My preference would be to avoid it for as long as possible and ask student to work directly with the descriptions. I’ve seen horrible exercises in textbooks about this.
I received this inquiry today. Can anyone help? Thanks, Gretchen
Do you know if the standards in a given math cluster are in a progression?
For example is 1, foundational to 2. etc..
We want to know the intent of the authors here.
No, there is no fixed scheme such as the one suggested above, although often there is some attempt to arrange the standards in an order that “tell the story” of the cluster, so to speak.
On page 23 of the OA progression document for Elementary, the Compare problem examples in the bottom row are very confusing. Are these problems intended to represent the “1/5 as much” type of language that is taught in 5th grade? Because no values are in them, it is difficult to decipher the intent of “A as much as the blue hat”. Could you clarify this language with an example including numbers? Each of these 3 types- Smaller unknown, Larger unknown and Multiplier unknown are all 5th grade we think. Could you clarify?
The types of problems are stated with the italic representing any phrase of the form “twice”, “3 times”, etc. Initially these problems will involve only whole numbers, and students could encounter such problems in Grade 4. For example, “A blue hat costs $B. A red hat costs twice as much as the blue hat. How much does the red hat cost?”.
representing any phrase of the form “twice”, “3 times”, etc. Initially these problems will involve only whole numbers, and students could encounter such problems in Grade 4. For example, “A blue hat costs $B. A red hat costs twice as much as the blue hat. How much does the red hat cost?”.
I am struggling with what liquid capacity measurement units should be taught in 4th and 5th grade. Third grade liquid capacity measurement units are clear, mL and liters. 4th and 5th grade COULD include customary liquid measurement. North Carolina “unpacked” the standards by including gallons, quarts, pints, etc. Arizona’s “unpacking” documents do not include the customary units for liquid capacity in these grades. Please help guide me in interpreting the CCSS intent with what liquid capacity units students should learn in 4th and 5th grade about. Thanks!
Chantelle,
I asked Dr. McCallum this same question via email before he provided this stream on his blog. This was his reply,
“Dear Leandra,
Throughout K-5 the standards carve out room for a focus on number and operations by limiting the spread of other topics, and that’s why capacity is not mentioned. Of course there are many contexts in which children might learn about gallons, pints, quarts, etc., including the home, and that which is not mentioned in the standards is not thereby forbidden, so teachers might well choose to use them as examples if they think the class is familiar with them. But the standards do not require class time to be spent on them.
Regards,
Bill McCallum”
Hope this helps.
Thank you Leandra!
I am excited about the focus on numbers and operations in the K-5 standards.
Leandra, thanks so much for posting this, it helps me enormously when others chime in if they have an answer!
G-CO.3 asks students to describe rotations and reflections that carry certain figures onto themselves. Is this standard really just rotational and reflective symmetry? A simple 360 degree rotation will always carry a figure back to itself, which seems much too simple for high school.
Yes, it refers for example to seeing that a 120 degree rotation around the circumcenter of an equilateral triangle takes it to itself.
Part 1: The 6-7 Ratios and Proportions progression document is quite clear about the intent to keep fraction notation and ratio notation distinct:
“Because ratios and rates are different and rates will often be written using fraction notation in high school, ratio notation should be distinct from fraction notation.” (page 4)
This makes sense for many reasons. However, this is a large departure from the norm. Keeping that in mind, critical area (1) in the Grade 6 standards introduction states:
“Thus students expand the scope of problems for which they can use multiplication and division to solve problems, and they connect ratios and fractions.” (page 39)
The phrase “connect ratios and fractions” really sounds like it is referring to fraction notation. Many people will interpret it that way due to it being the current norm. However, it seems more likely that this phrase is referring to the unit rate a/b of the ratio a : b, and possibly how you can generate fractional values in equivalent ratios. Is this correct? If so, the language in the Grade 6 standards introduction is very confusing and could mislead a large number of people. If this statement really does imply fraction notation, then I’m confused.
Part 2: Assuming students do not see fraction notation with ratios in Grade 6, how do the standard writers envision the flow from Grade 6 ratios to Grade 7 with proportions? Is it merely a distinction that they can write the values of these ratios as fractions, equate them, and then solve an equation? This seems to be brushed over in the progression document. Sure, proportions are not referred to in a standard, but the progression document does refer to them. Without this type of distinction, the progression document seems to contradict itself between grades. Am I missing something?
First, you are quite correct about separating fraction notation from ratio notation, and your interpretation of the sentence in the grade level introduction is correct. However, students in Grade 6 will still be using fractions in connection with ratio reasoning. See, for example, Method 3 in the margin on page 7, where students are seeing that you can get the second column by multiplying the first column by a fraction.
As for proportions, the emphasis in the standards is on understanding proportional relationships and using them to solve problems. Students know that proportional relationships are sets of equivalent ratios, and that equivalent ratios have the same unit rate. The cross-multiplying method is a consequence of this, but “setting-up-and-solving-proportions-by-cross-multiplying” is not a topic in itself, but rather a method that arises out of understanding proportional relationships. The discussion on the second half of page 9 is an attempt to explain this, but maybe it needs to be fleshed out.
I have taught most undergraduate college courses in mathematics and tutored at earlier levels. Simplification of fractions is important. Here are some examples of measure conversion, requiring simplification:
A pilot asked me to explain a formula he learned in flight school. His teachers there could not explain it. Here is the formula, with revised terminology:
A circular arc, radius r miles, angle A degrees, has length of arc approximately rA/60 miles.
I explained that the exact formula is rA* Pi/180 . (The fraction Pi/180 converts degree measure to radian measure.) Since Pi/180 is approximately 3/180 = 1/60, the flight school formula works. I asked him why not use the exact formula with a calculator. He laughed and said that the pilot has both hands on the controls; the calculation has to be mental. Here is an example of such a calculation. Suppose the arc has radius 80 miles, angle 70 degrees. The length of arc is approximately 80 * 70/60 = 80 * 7/6 = 40 \times 7/3 = 280/3 = 93 1/3 miles.
Calculating without simplification, the result is 5600/60 miles, a result that might not help the pilot.
Here is another example: I need a half-recipe, and the original called for 1/3 cup of flour. Now ½ * 1/3 = 1/6, so I need 1/6 cup of flour, but this is not a standard measure. I convert cups to tablespoons; there are 16 tablespoons in a cup. So 1/3 * 16 = 16/6. It would be tedious and inaccurate to measure 1/6 tablespoon 16 times. Simplifying, I get 8/3 = 2 2/3 tablespoons. I measure 2 full tablespoons and estimate 2/3 of another tablespoon. For more accuracy, use the fact that there are 3 teaspoons in a tablespoon: to get 2/3 tablespoon, measure 2 teaspoons. (Most American cooks have a set of measuring spoons: 1 tablespoon, and teaspoons: 1, ½, ¼, and 1/8.)
In many cases, fractions are most convenient and useful when simplified. Simplification is easier when a least common denominator is found. If fractions are multiplied, the simplification I easier when done before rather than after the multiplication.
Simplification of radicals is not in the Standards, and I agree with this omission. For example, I question the custom of expressing square roots with no perfect squares under the radical sign, such as
Sqrt(200) = 10 * Sqrt(2).
Young people may not know the old-fashioned reasons for this calculation. Before the era of calculators, people often used a table of square roots. Many tables showed square roots of the integers between 2 and 100. So you could not look up the square root of 200, but you could evaluate it as 10 Sqrt(2) approx. 10(1.414) = 14.14.
Furthermore, evaluation was often time-consuming and not very accurate. In addition to tables of square roots, we used slide rules and tables of logarithms. Say you wanted to evaluate:
(Equation 1) Sqrt (72) + Sqrt (2) approx. 8.585 + 1.414 = 9.899.
If you simplified Sqrt (72) as 6 Sqrt (2), then the result is 7 Sqrt (2), and you need to look up only one square root instead of two. Also, this calculation could be done on a slide rule, but the addition in Equation 1 could not. Today Equation 1 is done more accurately on a calculator; I like to do it with an exponent instead of a radical, like this:
72^.5 + 2^.5
Similarly, younger folks may not know a reason to rationalize denominators. For hand calculation, multiplication of decimals is usually easier than division. For example:
1/Sqrt(3) approx. 1/1.732
Rationalizing the denominator, you get Sqrt3)/3 approx 1.732/3.
By hand, the first calculation takes more time than second. The calculator is just as happy to divide as to multiply, so rationalizing of denominators is not as important as formerly.
Of course, another reason instructors demand simplified answers to is to get answers in a standard form, easier to grade. One way to get standard answers is to request a numerical answer, correct, say, to two decimal places. I like numerical answers, because they prepare the students for applied problems, and because I can make sure students know how to round decimals.
Rational expressions are sometimes simplified by finding a least common denominator and adding. For example, say f(x, y) is
1/(x + y) + 2/(x – y) + 3/(x^2 – y^2) = (3x + y + 3)/(x^2 – y^2)
The expression on the right is easier to evaluate than the one on the left. To motivate such simplifications, sometimes I ask the student to use each expression and a calculator to evaluate, say, f(1.96, 2.17).
If the student gets a common denominator by multiplying all three denominators, the result is
((x – y)( x^2 – y^2) + 2(x + y)( x^2 – y^2) +3(x + y)(x – y))/((x + y)(x – y)( x^2 – y^2))
This expression is awkward to write, let alone to evaluate. In the bad old days, before calculators, people had powerful reasons to simplify calculation. Even now, the effort can be worthwhile. As others have observed, if students are skilled with numerical fractions, they are more ready to learn algebraic fractions.
I don’t like any formula for adding fractions. The formulas are intimidating, and they don’t work well for adding more than two fractions. Instead, I like Lane’s comments on May 24, using primes. The hard part is finding the least common multiple; there is a nice discussion at http://mathforum.org/library/drmath/view/58140.html. One you have that number, it is not rocket science to rename each fraction with this denominator. Don’t state a formula or even a rule; just show some examples and let students practice until they catch on.
I prefer to say rename a fraction, rather than replace it with an equivalent fraction. In abstract algebra, we define fractions with an equivalence relation for ordered pairs of integers, so one pair can be equivalent to another. The pair (1, 2) is equivalent to the pair (2, 4). But the fractions ½ and 2/4 are not merely equivalent; they are equal; these are two names for the same number.
In middle and high school, students still need to practice fractions, including mixed numbers. In most textbooks I see, answers are small whole numbers, or decimals calculated with a calculator. Here is a use for fractions in algebra: graph by hand a linear equation in standard form, like 3x + 7y = 10. The fastest way to do so is to calculate the two intercepts, which are (3 1/3, 0), and (0, 1 3/7). Plot the two points on grid paper and connect with a straight edge. Note that these mixed numbers are easier to plot than the improper fractions, 10/3 and 10/7.
We compete economically, and we may compete in war, with nations whose curriculums include simplification of fractions. Members of the Armed Services are expected to know this topic. Community colleges have remedial courses, which include it. Contractors, carpenters, plumbers, and electricians need it. They should know 4/64 inch = 1/16 inch. In short, simplification of fractions is still essential.
Having had similar teaching experience, I have slowly bought into the rationale behind the CCSS on these points. Simplifying is really a misnomer in most cases. It may sound like splitting hairs, but that word confuses a lot of students because it is used in so many different contexts, meaning so many different things. With regards to reducing fractions, it is a very good practice; but we have too many students who can’t handle all the bells and whistles when they are thrown in too soon. I see the wisdom in always hammering the “one thing that always works” as far as multiplying denominators for those kids who get confused trying to remember all the methods that could be used. Be sure to finish reading that thread for LCD in the comments as we had quite a discussion before I decided CCSS has it right on that one, too.
One problem with “simplify” is that it suggests that there is a canonical simplified form of very expression. Choosing a form should have something to do with having a purpose. So, for example, the airline pilot wants to know about how many miles the arc is, and therefore it makes sense to write the fraction in the form of a mixed number.
Sorry I don’t have time right now to respond at greater length; thanks Lane for joining in!
Bill:
Several of the California Mathematics Project (CMP) sites are holding institutes on mathematical modeling. At one of the sites I’m visiting, the leaders asked me about the difference between mathematical modeling and the Standard for Mathematical Practice (SMP) “Model with Mathematics.” Some teachers think these are different concepts, and I’ve been told different things.
This is my perspective, and I want to know if this is the intent of the CCSS. Mathematical modeling is similar to the types of problems that CoMap has produced. The SMP model with mathematics is also connected to that definition. If one has a contextual problem, then model with mathematics is using mathematics to solve the problem, using mathematics as the model to solve the problem, then going back to the context. What it is not is using physical models to represent the problem.
I’ve heard in conferences the latter for model with mathematics–using physical models to represent the problem. Could you help me understand the difference between mathematical modeling and model with mathematics? Thanks.
Susie
Susie,
Your interpretation is correct. SMP 4 is as you describe, and is also as described on pages 72–73 of the standards, at least in high school. The phrase “mathematical modeling” refers to this as well.
However, in the elementary standards, there are standards like:
I think this is the source of the confusion, because it seems to be going the other way, using a physical situation to model a mathematical idea. Personally, I think the underlying process is quite similar; you are taking some problem you don’t know how to solve, modeling it with things you can manipulate (in this case, base ten blocks, later on, algebraic symbols), and using them to solve the problem. True, a two-digit addition is not a contextual problem, although in elementary school it will often arise out of one.
My algebra team and I are looking at the next year’s curriculum planning and I wonder if you can answer some questions. Using Arizona’s “suggested” levels it seems that rational expressions is meant for algebra 1 (9th grade) and SOLVING quadratics has been moved up to Algebra 2. Yet the rough PARCC framework states “working with linear, quadratic…..expressions and equations” and that Algebra 2 “expands knowledge…through rational expressions”. Is there any more clarity on either one of these ends? I think I heard that the frameworks will be released this fall. ….(?) Any direction you could offer would be awesome. I know things are still in a bit of flux and this year is a transition year anyway, but I would certainly feel better equipped to handle the barrage of questions that will be sent MY way this year so.. I’m adding to your barrage this summer
Cathey, since Arizona is a PARCC state my guess is that it will eventually conform to the PARCC framework when that becomes final. I guess the draft framework is a good guide to where they are heading, but state feedback might still cause some modifications. Sorry I can’t offer any more guidance!
Hi Bill,
I have a question on 4.OA.3
Solve multistep word problems posed with whole numbers and having whole-number answers using the four operations, including problems in which remainders must be interpreted. Represent these problems using equations with a letter standing for the unknown quantity. Assess the reasonableness of answers using mental computation and estimation strategies including rounding.
When it says “represent these problems using equations,” does this mean that the students need to formally solve an equation to solve the problem?
It doesn’t seem like it should, but I’ve seen questions “aligned” to this standard expecting an algebraic solution.
Erin, you answered your own question correctly! The standard does not say “solve”, it says “represent”. Of course, this is intended to be preparation for solving, since a numerical solution for a word problem will often track the algebraic solution to the equation.
Hi Dr. McCallum,
This discussion (paraphrased) has recently come up on our K-5 mathematics wiki-
“Concerning 5.OA.1: Use parentheses, brackets, or braces in numerical expressions, and evaluate expressions with these symbols.The Progressions document states, “In Grade 5, this work should be viewed as exploratory rather than for attaining mastery; for example, expressions should not contain nested grouping symbols and they should be no more complex than the expressions one finds in a application of the associative or distributive property, e.g., (8 + 27)+2 or (6 x 30) + (6 x 7)”. Would you clarify how this standard should be taught? How do you teach brackets, parentheses, and braces without nesting them within an equation or expression? Aren’t they hierarchical in nature?” I went out hunting, and here’s what the North Carolina explanation says: “Mathematically, there cannot be brackets or braces in a problem that does not have parentheses. Likewise, there cannot be braces in a problem that does not have both parentheses and brackets.”
I understand the confusion being generated here, and would love to have your thoughts on the matter. If you want to respond directly on the wiki (If not, I’ll cut and paste!)
– here’s the link- http://ccgpsmathematicsk-5.wikispaces.com/
The question is posted in the discussion forum on the home page.
Thanks so much. I truly appreciate the difference you are making.
Best,
Turtle
I have been sitting here reading through this entire thread for the past hour trying to see if someone else asked this question already before I post it…finally at the end of this page I see it. 🙂 I Have the same question and I am not clear whether there is even a point to addressing brackets and braces given the specific examples provided in the progression document. It almost sounds like the brackets and braces would replace the parenthesis (since the word “or” is used in the standard) but that doesn’t make sense as per Turtle’s explanation. With that being said, it is clear that this standard is addressing the big idea of students seeing the structures of and meaning behind the numerical expressions (MP7).
That’s how I see it, too, Jessica. Thanks for the affirmation.
Jessica’s answer is correct here. In general students in Grade 5 will be using parentheses only, because the convention about nesting that you describe is quite common, and it’s quite possible that instructional materials at this level wouldn’t even mention brackets and braces. However, the nesting order is only a convention, not a mathematical law; the North Carolina statement isn’t quite right here. It’s important to distinguish between mathematical laws (e.g. the commutative law) and conventions of notation (e.g. nesting of parentheses). Some conventions of notation are important enough that you want to insist on them in the classroom (e.g. order of operations). But I don’t think correct nesting of parentheses falls into that category. The main point of the standard is to understand the structure of numerical expressions with grouping symbols.
Thanks, Bill!
The standards in the Number System Domain in the 6th Grade dealing with rational numbers all use integers in the examples. Since the definition of a rational number given in that domain is “a point on the number line” is seems to make sense that we should be addressing fractions and decimals, both positive and negative, in building understanding about the number system. I can’t see students being able to add, subtract, multiply and divide rationals in the seventh grade without that understanding. So am I putting too much weight on the examples and not enough on the wording of the standards, or are we really intended to only extend the number system to integers as a part of the rational numbers?
That is a good lead in to my question about 7.EE.1. Is the use of the term rational coefficient meant to keep from limiting students to working only with integers or was it a push to working with negative and positive fractions and mixed numbers exclusively? NY State Education Dept says that “the intent of 7.EE.1 is being aware of the property used to factor a linear expression with rational coefficients, not just on the ability to factor a linear expression.” The sample question they give is ” Which expression is equivalent to (4/3)x + 4 2/3?” I think they’re interpreting rational coefficients to mean rational coefficients that are not integers. Was that truly the original “intent”?
After reading earlier posts about “simplifying” and the general form for addition of fractions, I’m now wondering if “factoring” would also be driven by context. The correct multiple choice response to that question has kids factor using the GCF of 2/3, but 1/3(4x + 14) or 2((2/3)x + 2 1/3) would be factors of the expression too. Then I began to think about the language being used in the question versus the language being used in the rationale. Which expression is equivalent doesn’t really ask students to factor. They can find the correct answer by applying the distributive property to each of the answers looking for the one that matches. I guess if I’m doing my job right and helping kids to see things in context, then my students would understand equivalent and be able to use an appropriate strategy. I think I was trying to factor it because I saw that all the answers were in the form a(bx + c) and I was programmed to find the GCF.
New question… Is 7.EE.1 a call for students to be flexible in their thinking? If the item writers weren’t so focused on “factoring” could that question have been changed to:
Which expression is not equivalent to (4/3)x + 4 2/3?
A (4/3)x + 4 + 2/3
B (4/3)x + 2(2 1/3)
C (4/3)(x + 2)
D (2/3)(2x + 7)
which would assess student’s ability to add, subtract, multiply, factor and/or expand a linear expression?
I’m very concerned though about the way that teachers across the country are going to be interpreting each standard and/or reacting to other’s (State Education Departments…) interpretations. The progression documents are helpful, but when State Ed contradicts the progression document, what do you do? I’ve been thinking and reacting to this one question for a while and I stumbled across this thread which helped me to process it further. I’m overwhelmed to the point of shutdown by the prospect of writing a years worth of curriculum this summer and feel as though I don’t have enough coherent resources to help me.
The examples are not intended to limit the standards to negative integers only. The standards do encompass all rational numbers. Since negative numbers are first introduced in Grade 6, it makes sense to start with negative integers for the sake of simplicity, but students should not finish Grade 6 without having seen other negative rational numbers. There is, however, a subtlety that doesn’t get taken up until Grade 7, namely the fact that .
.
I share this concern over interpretations. The Core isn’t common if there is widespread misinterpretation…and clearly there is. At this time, to understand the Standards, I think one must also read the progressions and these comments…and I’m still not sure that guarantees clarity. I would like to see a tech writer take (for example) Progressions: 6-7 Ratios and Proportional Relationships and have a 6th grade teacher tell them what they think it says. If the interpretation does not square with the intent, edit. When the tech writer explains a standard such that 3-4 random 6th grade teachers can correctly interpret the meaning, that should clear up much of the confusion. Sure, it’s expensive and time consuming to develop such documentation, but textbook publishers and State authorities are generating volumes of conflicting documentation. The longer we take to generate clear official explanations, the more expensive it will be to clean up misinterpretations.
Good points, Lane. It’s a big job and a slow process, coming together around common standards.
I teach 5th grade math in Ohio and am having trouble finding a sequence to use with the common core. Does anyone know where I could locate one? Thank you!
Christina, have you looked at the progressions documents, published on this blog? Go to the main page and click on the progressions category down on the right hand side. They are not exactly what you are looking for, because they don’t say how to weave the different progressions together, but they might help some.
Bill,
Would you elaborate more on A-REI.4a, specifically, on what would be expected to derive the quadratic formula from this form (x – p)^2 = q. In Appendix A, this standard is included in the Integrated Pathway, Math II, Unit 3 (probably 1st semester). Perhaps you could offer an example assessment question/activity that would get to the heart of this standard? Are p and q to be considered variables or constants? Any help you can give is greatly appreciated!
Fred, p and q are constants here. So, for example, you can use the method of completing the square to transform into
into  and then solve the equation by setting
and then solve the equation by setting  equal to each of the square roots of
equal to each of the square roots of  . If you do this with literal constants in place of specific numbers,
. If you do this with literal constants in place of specific numbers, 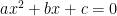 , you can derive the quadratic formula.
, you can derive the quadratic formula.
In the Common Core Standards App for iOS, the developers included a note on all of the (+) denoted standards that says: “(+) standards are included to increase coherence but are not necessarily expected to be addressed on high stakes assessments.” Is this an official stance from either your group or SBAC/PARCC? I cannot find that statement anywhere else. Do you suppose there is some amount of guessing involved?
I have read the interpretation of the (+) symbol in the actual standards document, but of course, assessments are not addressed there. My real question centers on the inclusion of some (+) standards in the Pathways (six of them by my count). This is a bit ambiguous, as they seem to be standards for both all students and for students preparing for advanced topics (doesn’t “all students” imply that already?). Thus, if they are for all students, wouldn’t it stand to reason that they could potentially be included on a high stakes assessment and the app’s note is misleading?
I know you have often directed questions about resources to the creators of said resources. So, perhaps I should ask instead for you to comment on your own beliefs/insights about the (+) which are included in the Pathways and the possibility that all students could possibly be assessed on these “advanced” topics. Thanks!
We’ll have to wait for the assessments to come out for the definitive answer to this, but notice the statement on page 57 of the standards:
So there is a distinction between what might appear in courses for all students and what might appear on the assessment. My guess is that (+) standards will not show up on the assessments, but we will have to wait and see.
Another specific standard question for you regarding N-CN.9. (+): Know the Fundamental Theorem of Algebra; show that it is true for quadratic polynomials.
Could you share your thoughts on the expectation of this standard? To “know” the theorem, is that to simply be able to state it? I have seen it written slightly differently – but is it too simplistic to know that a polynomial has the same number of roots as its degree? And what would constitute “showing” that it is true for quadratic polynomials? Thanks!
I think there’s more to “knowing” than “stating”; you also have to understand what you are saying, be able to explain what the theorem is saying, and so on. But this does not include proving the theorem (which is quite advanced!).
Also, you have to be careful about counting roots, since a polynomial can have a double root. One way to state the theorem is that every non-constant polynomial has a root in the complex numbers. This turns out to be equivalent to saying that a polynomial of degree n has n complex roots (where doubles roots are counted as 2, triples roots as 3 and so on).
Hello… recently at a meeting where we were looking at instructional materials to bridge CCSS implementation, we were having a discussion on the meaning of modeling. Modeling at the high school level is defined at the CCSS website, but my question is what does it look like at the elementary or middle school level? Do number lines count? How will we make sure that publishers are using the correct interpretation of Standard of Mathematical Practice #4?
If you use your browser to search for “modeling” in this thread you will find some discussion of this issue; let me know if it doesn’t answer your question.
I’m trying to write curriculum that incorporates the Statistics standards S.IC.1 – S.IC.6 (Making Inferences and Justifying Conclusions). I have looked in statistics texts that seem to have good information on this area, but I could use some help seeing what kind of depth is suggested. If students were to be tested on this at some future date, for instance:
– How much detail would they need?
– What kinds of questions would they be expected to answer?
Can anyone provide pointers in the right direction? Thank you!
With help, I found two links that address my question, so I thought I’d share them. I don’t think these provide complete answers, so I’m still interested in any other advice / suggestions out there.
http://www.dpi.state.nc.us/docs/acre/standards/common-core-tools/unpacking/math/statistics-probability.pdf
http://commoncoretools.me/wp-content/uploads/2012/04/ccss_progression_sp_hs_2012_04_21.pdf
Thanks Eric!
In working with teachers through professional development, I have come to realize that there is confusion about regular and irregular polygons as well as how to describe concave and convex mathematically (beyond that concave “caves in”). I don’t see these terms in the CCSSM explicitly, but have told teachers that they fall under “attributes” as described in the geometry standards.
In these discussions, I have suggested that teachers refer to other standards within their grade level to determine what is appropriate for their students. For example, describing a polygon as “regular” would come after understanding what it means for sides to be congruent and for angles to be congruent.
At what level do you see these ideas being appropriate based on the standards?
Julie
We did try to avoid lists of required terms at specific grade levels, because of the danger that such lists start to occupy too much attention from teachers and assessment writers, so that worrying about vocabulary obscures work on the mathematics. Consider, for example
You might use examples of both concave and convex polygons to illustrate different ways of calculating the area, by either decomposing it or viewing it as obtained by subtracting an area from a larger figure. But you might not spend too much time on the terms themselves, and the standards do not require that students know them.
Just wondering what is the standard algorithm for multiplication and division and how is it going to be tested!!! Thanks a bunch of teachers in Arkansas at a workshop
Dear Beth, there is lots written on this blog about the standard algorithm for multiplication: try searching on the term “standard algorithm” in this thread, and in the thread on Number and Operations in Base Ten. For the division algorithm, you might also look in the progression document itself.
I am looking for information or a link to pre-kindergarten math standards. Thanks!
There are no pre-kindergarten standards in the Common Core.
However, a number of states, including New York – http://www.p12.nysed.gov/ciai/common_core_standards/ and Massachusetts – http://www.doe.mass.edu/candi/commoncore/ have incorporated Pre-K into their states Common Core. Good luck.
Bill, we are having difficulty with the interpretation of G.M.G.1, 2, and 3 and the examples on illustrativemathematics.org are not very helpful. Can you provide a quick summary of each? And, are the students expected to know the formula for density or should that be given? Thanks!
Gee, not really sure what to say here except that we’ll work on more illustrations! The geometry progression when it comes out should help as well. I think I need to have a better idea of your specific questions here, otherwise I’ll just end up writing that part of the geometry progression, which I don’t have time for at the moment.
As for density, I guess I would say the concept and the formula are almost identical; for example, knowing the concept of (average) population density entails knowing that you would calculate it by dividing the population in an area by the area. In some sense it doesn’t matter whether the formula is given or not, because the student who knows how to make use of it won’t need it anyway.
why aren’t patterns included in the k curriculum?
This question has been discussed already in this thread; you can find the discussions by searching for the word “pattern” using your web browser’s search functionality while you have this thread open (not using the blog’s search feature).
Bill, looking at 2.NBT.5, 2.NBT.7 and 3.OA.5, I see that using the properties of operations are suggested to help add and subtract (Grade 2) and multiply and divide (Grade 3). The properties of addition and multiplication are easily understood but how are the properties of subtraction and division meant to be used?
On a different topic, 3.MD.6 asks students to measure area by counting unit squares and improvised units. What would improvised units include and why should students use them?
Hi Duane,
Re. improvised units –
An example of an improvised unit I’ve used in third grade is post-it notes. Students used them to cover their tables and other surfaces in the classroom. The goal of the lessons was not to get a standard measure of the area of the table, but to ensure students understood that area was a measure of coverage of the plane. It was also an opportunity to see if students had internalized the structure of arrays. Since the post-its were of a uniform size, we could also compare results.
Not an official answer, of course, but it might give you some ideas of avenues to take.
Karen
I’ve noticed that some standards incorporate the phrase “and/or”. For example, 3.NBT.2 “Fluently add and subtract within 1000 using strategies and algorithms based on place value, properties of operations, and/or the relationship between addition and subtraction.”
In this example, should “and/or” be interpreted as meaning that any of “place value”, “properties of operations”, and “the relationship between addition and subtraction” should only be used at any one time but all should be covered by the end of Grade 3? Or that you could use any combination of the three at one time? Or that it is okay if only one of them is covered by the end of Grade 3? And what would guide these decisions for teachers? Any of the approaches in 3.NBT.2 potentially could be used – I’m not sure if the expectation is to just use one or all of them.
Duane, replying to both comments here. I think you have to look at the entire sentence, e.g., in 2.NBT.5, “Fluently add and subtract within 100 using strategies based on place value, properties of operations, and/or the relationship between addition and subtraction.” The phrase “using strategies based on place value, etc.” qualifies the type of strategies to be used; the “and/or” is there because a given strategy might not be based on all of the things listed. The things listed are not a checklist to be covered by the end of a given grade; they constrain the type of strategies that students should be practicing. For example, counting on for addition is not a strategy based on place value, the properties of operations, or the relation between addition and subtraction. However, calculating 8+13 by breaking 8 into 1 + 7 and then adding the 7 to the 13 to get 20 and then adding the 1 is based on both place value (because you are focusing on what needs to be added to 3 to make 10) and on the properties of operations (because you are regrouping the addition from (1 + 7) + 13 to 1 + (7 + 13)). Calculating 81-73 by saying “I know I need to add 7 to 73 to get 80 and then 1 more to get 81, so the answer is 7 + 1 = 8” is based on place value and the relation between addition and subtraction (also implicitly on regrouping, but that’s a bit more subtle in this case).
I would point out that there is no standard requiring students to be able to state the properties of operations. However, they should be able to explain their strategies, and this will inevitably involve talking about the way operations work.
In studying the middle school Geometry standards, we have located where the formulas for area of most figures are developed but we are missing trapezoid. Can you point us in the right direction?
Also, volume of most 3-d figures is developed as well but pyramids are missing. Do they belong with prisms in grade 7 or with cylinders, cones, and spheres in grade 8?
Thanks
[Corrected 2013/07/07]
Some fundamental formulas for area are in the standards, but in many cases students are expected to find areas by decomposing figures, e.g.
A trapezoid counts as a special quadrilateral. Students who have calculated a few areas this way might begin to be able to see why the formula is true.
There’s no reason why pyramids couldn’t be included in Grades 7 or 8, although as you point out they aren’t explicitly required. Note that the “formula” is the same for both pyramids and cones, if you take it to be Volume = (1/3) x Area of Base x Height.
In high school, G-GMD.1, students are expected to understand at least informally why this is true. This line of reasoning actually starts with pyramids.
In 4.MD.1 it seems that students do conversions *only* from larger measurement units to smaller ones.
5.MD.1 appears to have students convert larger to smaller but also smaller to larger.
Is that a correct interpretation?
Yes, this is connected to the progression in fraction multiplication. Students don’t multiply quantities by fractions until Grade 5, so saying “an inch is 1/12 as a big as a foot” would be sort of jumping the gun in Grade 4.
Hello Dr. McCallum,
I am from Washington state, and we are beginning to roll out the CCSS standards this year for K-2. I currently teach second grade and am on a team that is working on scope and sequence along with benchmarking in needed areas. We are a fairly low income area, and knowledge of money is not something that a vast majority of our students have knowledge of or get practice with outside of our classroom. With money being taught in second grade, we take it very seriously since it is such a life skill. My question may be a stupid question, but when looking at 2.MD.8, working with time and money, it states that students need to work with dollars and cents.
I am assuming that when the standard speaks of “dollars” that we are including $1.00, $5.00, $10.00, $20.00, $50.00, and $100.00 bills? I saw the post earlier about teaching the dollars in whole amounts in conjunction with whole number addition and subtraction. And that makes total sense to me.
Our former state standard only had students making amounts with coins up to $1.00, so this is going to be a big transition for our teachers (and students). I will be going in to a meeting to train teachers who are new to standards based grading in August, and I would like to be able to answer questions about the standards as well as formative and summative assessments.
I really appreciate the forum and the outlet in which to get some clarity. I am excited about working with the new standards, but want to make sure that I am presenting things accurately with my colleagues, and most importantly, my students.
Best Regards,
Amanda
Amanda,
I’m not sure if you’re looking for suggestions on how to address money as a life skill (as opposed to a math skill) or not, but I’ll offer one up anyway.
I know teachers in our area are concerned about the de-emphasis on time and money in 2nd grade as compared to our state standards. I used to use money as part of my classroom management plan and it worked really well. It has the bonus of being able to focus on money year-round as well as using it in an authentic context.
What I describe was used with third graders, but it could easily be adapted to 2nd.
I gave each student a bank account and a checkbook. I initially used fake money, but there ended up being a rash of thefts. I liked the checks because they had to use the written form of the number.
Each student was paid for being a student, we’ll say $\$100$/wk. There were performance perks – turning in all homework on time all week might have gotten the child a $\$10$ bonus. There were fines for rule infractions; if they forgot supplies they purchased them from me. Occasionally I’d set up a store for them to shop for treats. We also had days in which they could set up their own store and bring in toys to sell to each other. Class rewards were based on their balance since that was a good indicator of behavior and responsibility e.g. Everyone who had a balance of $54 or greater could have lunch in the classroom.
Logistics – I asked my bank to donate some blank counter checks. You only need a few to copy. I kept the checks in a common pile because having each student keep up with their personal checkbook proved too complicated. They did have to keep up with their own register, though.
The system worked really well and provided lots of opportunity for math throughout the day. It also allows them to “discover” the concept of negative numbers as their accounts went into the red.
Karen
These are great ideas, Karen. In response to the concern about de-emphasizing time and money, I would say that there is no reason why time and money can’t be used to support the work on arithmetic. The point is that they are not topics in their own right in the mathematics curriculum, but they are certainly included in the possible contexts for word problems, measurement problems, etc.
Another question. (It’s been a busy few days!) In Grade 4, students use fractions with denominators limited to 2, 3, 4, 5, 6, 8, 10, 12, and 100 (according to the Standards, p.30). Yet in the relevant Progressions document (p.5) the example provided for comparison of fractions (4.NF.2) shows 96 as a common denominator for 5/8 and 7/12. Having other denominators outside the stipulated range are also likely when comparing, for example, thirds and fifths, fourths and tenths, and so on.
Is it the case that the example in the Progressions document is *not* one to use with students but is just meant to illustrate to teachers what is required? Or is it expected that students will need to tackle denominators outside the stipulated range for Grade 4?
Also, at the top of p.6 of the Progressions document on fractions is the third line down meant to begin “Grade 5 students…” or “Grade 4 students…”? Thanks!
P.S. Thanks Karen G (July 23) for the response about improvised units!
Duane, you are quite right that the Progression violates the restriction on what students are expected to work with here, and maybe we should use a different example. Although I would repeat the general comment I’ve made elsewhere that a restriction on expectations does not forbid the teacher from ever mentioning examples beyond the expectations. For example, a comparison between 2/3 and 3/5 might well come up in a Grade 4 classroom. The restrictions in the standards are intended to both restrict what can be put on an assessment, and to put the brakes on over-enthusiastic focus on one part of the standards; they aren’t intended to forbid the use of examples that time and common sense allow.
The “Grade 5” at the top of page 6 is correct. The idea is to point out that this common justification of the rule about equivalent fractions doesn’t really make sense until Grade 5, when students start to multiply fractions by fractions.
Message from concerned teacher…
I am in need of clarification about the extent of teaching 6th graders about inequalities. II have seen in some task and common core workbooks where the student is being asked to solve 1-step inequalities,but it is not explicitly stated in the standards (see below).
In the standards, I do not see where the 6th grade student is asked to specifically solve an inequality as they are asked to solve an equation.
The standard is specific about the type of equation the students should solve but does not indicate that the student has to solve an inequality.
My understanding of the standards is that students are being asked to:
* Identify from a given set whether a value is a solution of an
inequality. They are using substitution to find solutions of
inequality.
* Solve one-step equations
* Write inequalities given a specific situation
* Recognize that inequalities can have an infinitely number of solutions.
* Graph solution sets of inequalities on a number line.
6.EE.5. Understand solving an equation or inequality as a process of answering a question: which values from a specified set, if any, make the equation or inequality true? Use substitution to determine whether a given number in a specified set makes an equation or inequality true.
MCC6.EE.7. Solve real-world and mathematical problems by writing and solving equations of the form x + p = q and px = q for cases in which p, q and x are all nonnegative rational numbers.
MCC6.EE.8. Write an inequality of the form x > c or x c or x r or px + q < r, where p, q, and r are specific rational numbers. Graph the solution set of the inequality and interpret it in the context of the problem. For example: As a salesperson, you are paid $\$50$ per week plus $\$3$ per sale. This week you want your pay to be at least $100. Write an inequality for the number of sales you need to make, and describe the solutions.
Michelle, your understanding is correct, this is a good summary. Students are expected to solve one-step linear equations with positive coefficients and solutions; for inequalities, they are expected to work with and understand solutions in various ways, but not to actually solve them.
I was confused by your MCC6.EE.8. It seems to say that students should solve inequalities of the form px + q < r, which is not in the Grade 6 standards. Maybe it is a cut and paste error or maybe that is a place where your state added something to the standards (but did they really add these sorts of inequalities without also increasing the demand on equations?).
I noticed that in the illustrative mathematics example (8.G Find the Missing Angle) under 8.G.05 the Solution quotes as one of the steps “Since m and l are parallel, the alternate interior angles ZAX and AZB have the same measure”.
My question is: If part of the 8.G.05 standard is supposed to “establish facts about the angles created when parallel lines are cut by a transversal”, is it ok that the official names of the angles created (alternate interior, alternate exterior, etc) be used when assessing students knowledge of the facts established under this task?
The standards don’t mention the specific terms, so I think this is going to be up to curriculum designers to decide. And, of course, assessment writers will have some influence on this. That said, my feeling is that it’s going to be hard to talk about these things without introducing the standard terminology.
I asked a question earlier about the sequence of standards, the way they are sequenced in the CCSS document compared to the sequence that a classroom teacher might create. I do understand from page 5 that the sequence in the CCSS was not intended to be a rigid format for us to hold ourselves to. Our academic leaders have always given us given the liberty to decide what is best for the students within our classroom environment. I’d like to narrow my initial comment down to a more specific concern about the sequence of 5.NBT. Scenario: I teach 5.NBT.2 the first week, followed by 5.NBT.5-.6. Seven weeks later I teach 5.NBT.1 and 3,4,6,and 7 later on. In this case, it seems to me that NBT.1 would be a foundation that leads precedes NBT.2. The remaining standards within NBT would be at my discretion. As a classroom teacher, could you see the rationale for the sequence of NBT.2 before NBT.1? There is a lot of ground to cover with the CCSS and I want to make sure I do it justice on behalf of my students. Thank you in advance for your reply.
The place value understanding expressed in 5.NBT.1 is foundational to the rest of the standards. That said, note that it is part of a progression of standards from earlier grades, 1.NBT.2, 2.NBT.1, and 4.NBT.1. In particular, 4.NBT.1 says “Recognize that in a multi-digit whole number, a digit in one place represents ten times what it represents in the place to its right.” This is enough to support the part of 5.NBT.2 that deals with whole numbers. I can imagine a curriculum that threads its way through that part of the standard first, then comes back to the issue of decimals later.
Basically, the standards are not units of instruction; you don’t always “teach a standard” in one chunk, whatever the order. For example, the OA and NBT standards in any given great level are very closely related, and a curriculum might be touching on these two domains simultaneously at times, not to mention supporting standards in MD and other domains. The standards describe achievements we want students to have. As my colleague Jason Zimba likes to say, you don’t teach standards, you teach math.
Pingback: New forum | Tools for the Common Core Standards
Pingback: Tips on searching this blog | Tools for the Common Core Standards